MatheGrafix Hilfe | Galerie Klassische Fraktale II

Formel: z_n+1 = e^-z_n²+c → MatheGrafix 12-Datei	Formel: z_n+1 = z_n+2^z_n+1+c → MatheGrafix 12-Datei	Formel: z_n+1 = z_n²+im(z_n-1)+c → MatheGrafix 12-Datei
Formel: z_n+1 = cos(z_n)+c → MatheGrafix 12-Datei	Formel: z_n+1 = tan(z_n²+c) → MatheGrafix 12-Datei	Formel: z_n+1 = z_n²+im(z_n-1)+c → MatheGrafix 12-Datei

Glynn-Fraktal: z_n+1 = z_n^1,5+c Auch Baum des Lebens genannt! → MatheGrafix 12-Datei	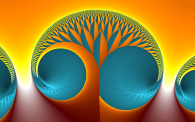Formel: z_n+1 =z_n^1,5-c² → MatheGrafix 12-Datei	Formel: z_n+1 =z_n^1,5-c² → MatheGrafix 12-Datei
Glynn-Fraktal: z_n+1 = z_n^1,5+c → MatheGrafix 12-Datei	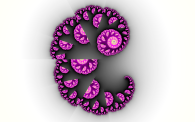Formel: z_n+1 = z_n^1,5-conj(c) → MatheGrafix 12-Datei	Formel: z_n+1 = z_n^1,5-c³ → MatheGrafix 12-Datei
Celtic z_n+1 = abs(re(z_n²))+im(z_n²)+c → MatheGrafix 12-Datei	Celtic → MatheGrafix 12-Datei	Celtic → MatheGrafix 12-Datei
Formel: z_n+1 = c*sin(z_n) → MatheGrafix 12-Datei	Formel: z_n+1 = c*sin(z_n) → MatheGrafix 12-Datei	Formel: z_n+1 = z_n²+im(z_n-1)+c → MatheGrafix 12-Datei
Formel: z_n+1 = tan(z_n²+c) → MatheGrafix 12-Datei	Formel: z_n+1 = tan(z_n²+c) → MatheGrafix 12-Datei	Formel: z_n+1 = z_n²-z_n-1²+c → MatheGrafix 12-Datei

MatheGrafix 12 / Online-Hilfe