Startseite 
Online-Hilfe 
Impressum, Datenschutz Galerie Raummodul - Rotationskörper
Diese spezielle Galerie zum Raummodul zeigt den Weg von der Funktion zur Parameterdarstellung der Mantelfläche des Rotationskörpers. Ein Rotationskörper lässt sich in der MatheGrafix 12-Datei von allen Seiten betrachten, er kann auch automatisch "rotieren".
Bei den folgenden Beispielen wird die Variable x einer Funktionen mit der Variablen u ersetzt, um den Zusammenhang mit der Parameterdarstellung deutlich zu machen.
Bei den folgenden Beispielen wird die Variable x einer Funktionen mit der Variablen u ersetzt, um den Zusammenhang mit der Parameterdarstellung deutlich zu machen.
1. Zylinder und Kegel - Strecken
1.1 Zylinder: Eine Strecke, die parallel zur x-Achse verläuft, rotiert um die x-Achse
|
Theorie
Strecke: f(u) = 2, Df = [1,5]
→ Hilfe
Parameterdarstellung • x(u,v) = 2 *sin(v) • y(u,v) = u • z(u,v) = 2 *cos(v) mit u von 1 bis 5, v von 0 bis 2π |
Mantelfläche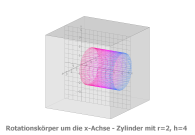
→ MatheGrafix 12-Datei |
Andere Darstellung
→ MatheGrafix 12-Datei |
1.2 Kegel: Eine Strecke rotiert um die x-Achse
|
Theorie
Strecke: f(u)=-3/5*u+3, Df=[0,5]
→ Hilfe
Parameterdarstellung • x(u,v) = (-3/5*u+3) *sin(v) • y(u,v) = u • z(u,v) = (-3/5*u+3) *cos(v) mit u von 0 bis 5, v von 0 bis 2π |
Mantelfläche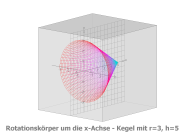
→ MatheGrafix 12-Datei |
Andere Darstellung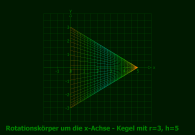
→ MatheGrafix 12-Datei |
1.3 Kegel: Eine Strecke rotiert um die y-Achse
|
Theorie
Strecke: f(u)=-3/2*u+3, Df=[0,2]
→ Hilfe
Parameterdarstellung • x(u,v) = u*sin(v) • y(u,v) = u*cos(v) • z(u,v) = -3/2*u+3 mit u von 0 bis 2, v von 0 bis 2π |
Mantelfläche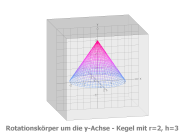
→ MatheGrafix 12-Datei |
Andere Darstellung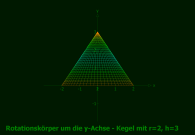
→ MatheGrafix 12-Datei |
2. Normalparabel
2.1 Die Normalparabel rotiert um die x-Achse
|
Theorie
Funktion: f(u) = u^2, Df = [-2,2]
→ Hilfe
Parameterdarstellung • x(u,v) = u^2 *sin(v) • y(u,v) = u • z(u,v) = u^2 *cos(v) mit u von -2 bis 2, v von 0 bis 2π |
Mantelfläche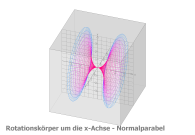
→ MatheGrafix 12-Datei |
Andere Darstellung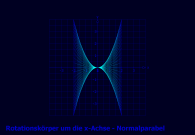
→ MatheGrafix 12-Datei |
2.2 Die Normalparabel rotiert um die y-Achse
|
Theorie
Funktion: f(u) = u^2, Df = [0,2]
→ Hilfe
Parameterdarstellung • x(u,v) = u*sin(v) • y(u,v) = u*cos(v) • z(u,v) = u^2 mit u von 0 bis 2, v von 0 bis 2π |
Mantelfläche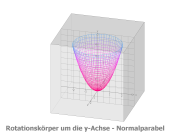
→ MatheGrafix 12-Datei |
Andere Darstellung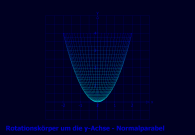
→ MatheGrafix 12-Datei |
3. Kugel und Halbkugel - Wurzelfunktionen
3.1 Kugel: Eine Wurzelfunktion rotiert um die x-Achse
|
Theorie
Funktion: f(u) = Sqrt(9-u^2),
→ Hilfe
Df = [-3,3] Parameterdarstellung • x(u,v) = Sqrt(9-u^2) *sin(v) • y(u,v) = u • z(u,v) = Sqrt(9-u^2) *cos(v) mit u von -3 bis 3, v von 0 bis 2π |
Mantelfläche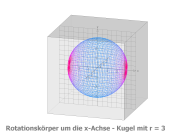
→ MatheGrafix 12-Datei |
Andere Darstellung
→ MatheGrafix 12-Datei |
3.2 Halbkugel: Eine Wurzelfunktion rotiert rotiert um die y-Achse
|
Theorie
Funktion: f(u) = Sqrt(4-u^2),
→ Hilfe
Df = [0,2] Parameterdarstellung • x(u,v) = u*sin(v) • y(u,v) = u*cos(v) • z(u,v) = Sqrt(4-u^2) mit u von 0 bis 2, v von 0 bis 2π |
Mantelfläche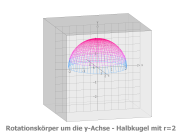
→ MatheGrafix 12-Datei |
Andere Darstellung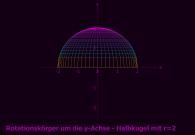
→ MatheGrafix 12-Datei |
4. Flasche - Splines
4.1 Flasche: Eine Splinefunktion rotiert um die x-Achse
Im Datenmodul unter "1. Dateneingabe" wurden in der Tabelle DatA Punkte eingegeben, die von einer Flasche abgenommen wurden.
Unter "2. Regression" wurden die Punkte mit Splines verbunden. Die entstandene Funktion heißt in MatheGrafix f(x) = Spline_DatA(x).
Nach dem Umschalten in das Raummodul steht diese Funktion auch im Raummodul zur Verfügung:
|
Theorie
Funktion: f(u) = Spline_DatA(u),
→ Hilfe
Df = [0,85;16,9] Parameterdarstellung • x(u,v) = Spline_DatA(u) *sin(v) • y(u,v) = u • z(u,v) = Spline_DatA(u) *cos(v) mit u ∈ [0,85;16,9], v ∈ [0;2π] |
Mantelfläche
→ MatheGrafix 12-Datei |
Andere Darstellung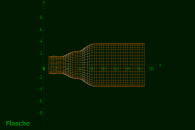
→ MatheGrafix 12-Datei |
