MatheGrafix 12 / Online-Hilfe

Auswertung einer Datenreihe zum logistischen Wachstum

Als Beispiel dient das logistische Wachstum einer bestimmten Hefemenge N(t) zur Zeit t.

1. Etwas Theorie: Die logistische Wachstumsfunktion

Eine Möglichkeit zur Darstellung ist die Formel y(t) = y₀∙S / (y₀+(S-y₀)∙exp(-S∙k∙t)), dabei gilt:
   t:      Zeit
   y(t):  Bestandsgröße nach t Zeitschritten
   S:     natürliche Schranke, Sättigungsgrenze
   k:     Wachstumskonstante
   y₀:    Anfangsbestand zur Zeit t=0
Diese Formel eignet sich besonders wegen der in MatheGrafix vorgebbaren Genauigkeit auf die wesentlichen Stellen (siehe 3.).

2. Dateneingabe

Die Messreihe steht als csv-Datei zum Download bereit:
hefewachstum.csv
Diese CSV-Datei wird unter dem Reiter "1. Daten eingeben" in die aktuelle Tabelle von MatheGrafix importiert:

• Im Feld "Daten eingeben" wählt man die Tabelle DatA. Über den Button Import CSV liest man die Datei ein.
• Mit dem Button Achsen anpassen passt man die Einheiten im Koordinatensystem an.
• Die Achsenbeschriftung im Koordinatensystem erhält man mit dem Button Übertragen.
• Im rechten Grafikfenster stellt man unter dem Reiter "Gitterlinien" noch Millimeterpapier ein.

3. Funktionsgleichung zum logistischen Wachstum

Unter dem Reiter "2. Regression" kommt man mit dem Button Logistisches Wachstum zum Eingabedialog für die Sättigungsgrenze. Diese wird bei vielen Aufgaben vorgegeben, MatheGrafix berechnet aber auch die optimale Sättigungsgrenze!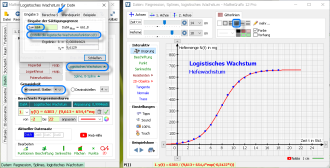

• Eingabe der Sättigungsgrenze und Erstellen der logistischen Wachstumsfunktion
  In diesem Beispiel wird die Sättigungsgrenze S vorgegeben, hier mit 664. Diesen Wert gibt man im Dialogfeld für S ein und klickt auf den Button
  Erstelle die logistische Wachstumsfunktion y(t). Man erhält
  y(t) = 6383 / (9,613+ 654,4*exp(-0,5422*t)),
  wobei die Genauigkeit auf 4 wesentliche Stellen eingestellt ist.
• Ablesen der Parameter
  Bei der von MatheGrafix gelieferten Funktion kann man die Parameter nicht direkt ablesen, da aus Gründen der Genauigkeit zuerst multipliziert und dann gerundet wurde. Die Parameter findet man allerdings im Eingabedialog für die Sättigungsgrenze:
     S   = 664
     k   = 0,000816621
     y₀  = 9,6129 (angepasst an die Messreihe)
     Wendepunkt W(7,78367|332)
• Berechnen der Sättigungsgrenze
  Ist die Sättigungsgrenze nicht bekannt oder ist die den Daten entsprechende optimale Sättigungsgrenze gesucht, rechnet MatheGrafix diese aus:
  Die optimale Sättigungsgrenze erhält man im Eingabedialog für die Sättigungsgrenze unter dem Reiter "Berechne S" mit dem Button 1. Berechne die optimale Sättigungsgrenze S.
  Dieser Wert wird erst mit dem Button 2. Übertrage S in die Eingabe und erstelle y(t) für die Erstellung der logistischen Funktion übernommen.

4. Das fertige Beispiel findet man in MatheGrafix und in der Datei

hefewachstum.mg12