MatheGrafix 12 / Online-Hilfe

Auswertung dreier Messreihen zum Ohmschen Gesetz

Drei Messreihen zeigen das Verhalten von Spule, Widerstand und Glühlampe im Gleichstromkreis.

1. Dateneingabe

Die drei Messreihen stehen als CSV-Dateien zum Download bereit:
spule.csv      widerstand.csv      gluehlampe.csv

Import der Daten
Die CSV-Dateien werden nun der Reihe nach unter dem Reiter "1. Dateneingabe" in die Tabellen von MatheGrafix importiert:

• Im Feld "Daten eingeben" wählt man die Tabelle DatA. Über den Button Import CSV liest man die Messreihe für die Spule ein.
  Damit die Datenpunkte sichtbar werden, passt man mit dem Button Achsen anpassen die Einheiten im Grafikfenster an. Die Farbe der gezeichneten Punkte stimmt mit der Farbe des entsprechenden Tabellenreiters überein.
  Die Achsenbeschriftung im Grafikfenster erhält man mit dem Button Übertragen.
• Nun wählt man die Tabelle DatB und liest die Messreihe für den Widerstand ein.
• In die Tabelle DatC kommt die Messreihe für die Glühlampe.
  Jetzt passt man nochmal die Einheiten mit dem Button Achsen anpassen an.

2. Regression (Ausgleichsrechnung) und Bestimmung von R in mΩ

Für die drei Datensätze werden nun unter dem Reiter "2. Regression" die Ausgleichsgeraden bzw. Kurven bestimmt.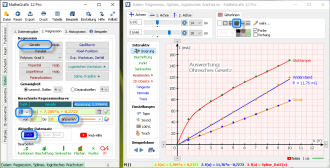

• Im Feld Aktueller Datensatz wählen Sie den Datensatz DatA für die Spule aus.
  Im Feld "Berechnete Regressionskurve" sollte die 1. Funktion ausgewählt sein:
  Mit dem Button Gerade erhält man die entsprechende Ausgleichsgerade. Mit dem Button anpassen im Feld "Berechnete Regressionskurve" passt man den Definitionsbereich der Funktion an den Bereich der Punkte an.
• Nach Auswahl des Datensatzes DatB für den Widerstand und der 2. Funktion erhält man mit dem Button Gerade die passende Ausgleichsgerade f(x) = 11,76*x - 0,7273.
  Die Steigung dieser Geraden liefert den Wert für den Widerstand R = 11,76 mΩ.
• Die Datenpunkte der Glühlampe DatC liegen leider nur im rechten Teil auf einer Geraden. Es gibt daher keine passende Ausgleichsgerade.
  Nach Auswahl des Datensatzes DatC und der 3. Funktion erhält man mit dem Button Spline, B-Spline immerhin eine Verbindung der Punkte und als 3. Funktionsgleichung f(x) = splineDatC(x). Das bedeutet, dass zum Datensatz DatC die entsprechende Spline-Kurve gezeichnet wird.
  Aber auch diese Kurve ist nicht optimal, da eine Spline-Kurve genau durch die Punkte geht. Dieses Verhalten lässt sich mit einem B-Spline abmildern. Durch die Eingabe des Glättungsfaktors "0,0001" für den B-Spline erhält man eine bessere Näherungskurve.

3. Das fertige Beispiel findet man in MatheGrafix unter dem Reiter "Beispiele" und in der Datei

ohmsches_gesetz.mg12