MatheGrafix 12 / Online-Hilfe

Auswertung einer Messreihe zum freien Fall

Für jeden Fallweg s wurden drei Messungen für die Zeit t durchgeführt. Man erhält damit für jeden Fallweg s drei Messpunkte für t im Graphen!

1. Dateneingabe

Die Messreihe steht als csv-Datei zum Download bereit:
freier_fall.csv
Diese CSV-Datei wird unter dem Reiter "1. Dateneingabe" in die aktuelle Tabelle von MatheGrafix importiert:

• Im Feld "Daten eingeben" wählt man die Tabelle DatA. Über den Button Import CSV liest man die Datei ein.
• Damit die Datenpunkte optimal dargestellt werden, stellt man im rechten Grafikfenster die Breite auf 18cm und die Höhe auf 15cm ein.
• Danach passt man mit dem Button Achsen anpassen die Einheiten im Grafikfenster an.
• Die Achsenbeschriftung im Koordinatensystem erhält man mit dem Button Übertragen.
• Im rechten Grafikfenster stellt man unter dem Reiter "Gitterlinien" noch Millimeterpapier ein.

2. Regression (Ausgleichsparabel) und Bestimmung der Gravitationskonstante g

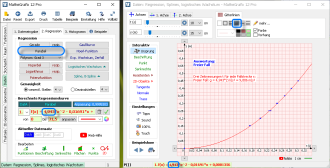Unter dem Reiter "2. Regression" erhält man mit dem Button Parabel die Ausgleichsparabel
f(x) = 4,943*x^2 - 0,01691*x + 0,0001356.
Mit der Formel s(t) = ½gt² + v₀t + s₀ (wobei beim Start
v₀ = 0 m/s und s₀ = 0m sind) erhält man für
g = 2 * 4,943 m/s² bzw. g = 9,886 m/s².

3. Das fertige Beispiel

findet man in MatheGrafix und in der Datei
freier_fall.mg12