Startseite 
Online-Hilfe 
Impressum, Datenschutz 3D-Ljapunow-Diagramme
Durchwanderm von Ljapunow-Diagrammen in der dritten Dimension
Durchwandern von Ljapunow-Diagrammen in der dritten Dimension
Information (Die Werte a,b und der neue Wert c für den Parameter r)
Mathematik
Als Iterationsformel dient die logistische Gleichung mit einem Parameter r:
Für die Konstante r wählt man klassisch die Konstanten a und b. Die Reihenfolge, mit der sich diese Konstanten abwechseln, wird als Sequenz vorgegeben, z. B. bbaba.
Zu den Werten a und b kommt für die dritte Dimension der Wert c hinzu - ein Schieberegler läuft in MatheGrafix automatisch durch die Werte von c. Eine Sequenz, die diese Werte benutzt, ist z.B. abcc mit geeigneten Wertebereichen für a und b (die Ebene) sowie geigneten Werten für c (die Höhe).
Für jeden Wert von c erhält man ein Bild der ba-Ebene in Höhe von c.
Tipp: Die Theorie der Ljapunow-Diagramme für mehrere Dimensionen findet man auf WIKIPEDIA.
Für die Erstellung eines Ljapunow-Diagramms in drei Dimensionen mit der logistischen Gleichung (bei den anderen Formeln dauert der Bildwechsel sehr lange) sind fünf Vorgaben erforderlich:
- Sequenz: Hier gibt man die eben erwähnte Reihenfolge der Konstanten a, b und c ein.
- Vorlauf (Schritte): Ohne Berechnung des Ljapunow-Exponenten λ werden in dieser "Warmup-Phase" die Folgeelemente berechnet, damit sich das Verhalten der Folge schon "einpendeln" kann.
- Maximale Schritte n: Die maximale Anzahl der Schritte zur Berechnung des Ljapunow-Exponenten λ wird angegeben.
- Zeichenbereich für a und b: Der Zeichenbereich für die ba-Ebene (≙ Wertebereichen von a und b) ist jeweils von 2 bis 4 vorgegeben, kann aber beliebig geändert werden.
-
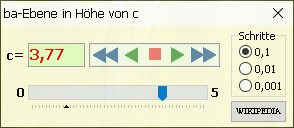Wert für c: Mit einem Klick auf den Button c erscheint ein Schieberegler, mit dem man den Wert von c auf einen Wert zwischen 0 und 5 einstellen kann. Diesen Schieberegler kann man auch automatisch vor und zurück laufen lassen, dabei erhält man für jeden Wert von c ein Bild der ba-Ebene.
Im linken Feld des Hauptfensters findet man einige Beispielbuttons mit "c". Mit diesen Buttons wählt man Beispiele mit interessanten Sequenzen für a, b und c aus.
