MatheGrafix 12 / Online-Hilfe

Aufgabe: Vorgegebener Ablehnungsbereich, Berechnung des Fehlers 1. Art

Bei einem Test werden 25 Fragen gestellt, die mit ja oder mit nein zu beantworten sind. Der Prüfer vermutet, dass sich ein Prüfling nur aufs Raten verlässt. Um seine Vermutung zu testen, greift er zu folgender Entscheidungsregel: Gibt der Prüfling mehr als 15 richtige Antworten an, so geht der Prüfer von seiner Vermutung ab. Wie groß ist die Wahrscheinlichkeit, hierbei eine Fehlentscheidung zu treffen?

Lösung

Bestimmung des Signifikanzniveaus mit den Tabellen der Binomialverteilung und mit der Näherungsformel von de Moivre-Laplace:

• Stichprobenumfang: n = 25
• Treffer bedeutet: Der Prüfling hat die Frage richtig beantwortet bzw. richtig geraten.
• Zufallsgröße X: Anzahl der Treffer bzw. der richtig beantworteten Fragen
• X ist bei wahrer Nullhypothese B_25;0,5-verteilt.
• Die Hypothesen lauten: H₀:p ≤ 0,5 (Es wird nur geraten!) und H₁:p > 0,5.
  Da große Werte von X gegen H₀ sprechen, handelt es sich um einen rechtsseitigen Test (folgt auch nach der alten Bauernregel). Kleine Werte von X sprechen in diesem Fall eher für H₀, daher handelt es sich nicht um einen beidseitigen Test. Allerdings findet man in vielen Lösungsvorschlägen auch H₀:p = 0,5.
• Der Ablehnungsbereich ist vorgegeben mit {16,17,18,...,25}.
  
  
• Bestimmung des Ablehnungsbereichs:
  • Methode 1: Lösung mit den Tabellen der Binomialverteilung
    
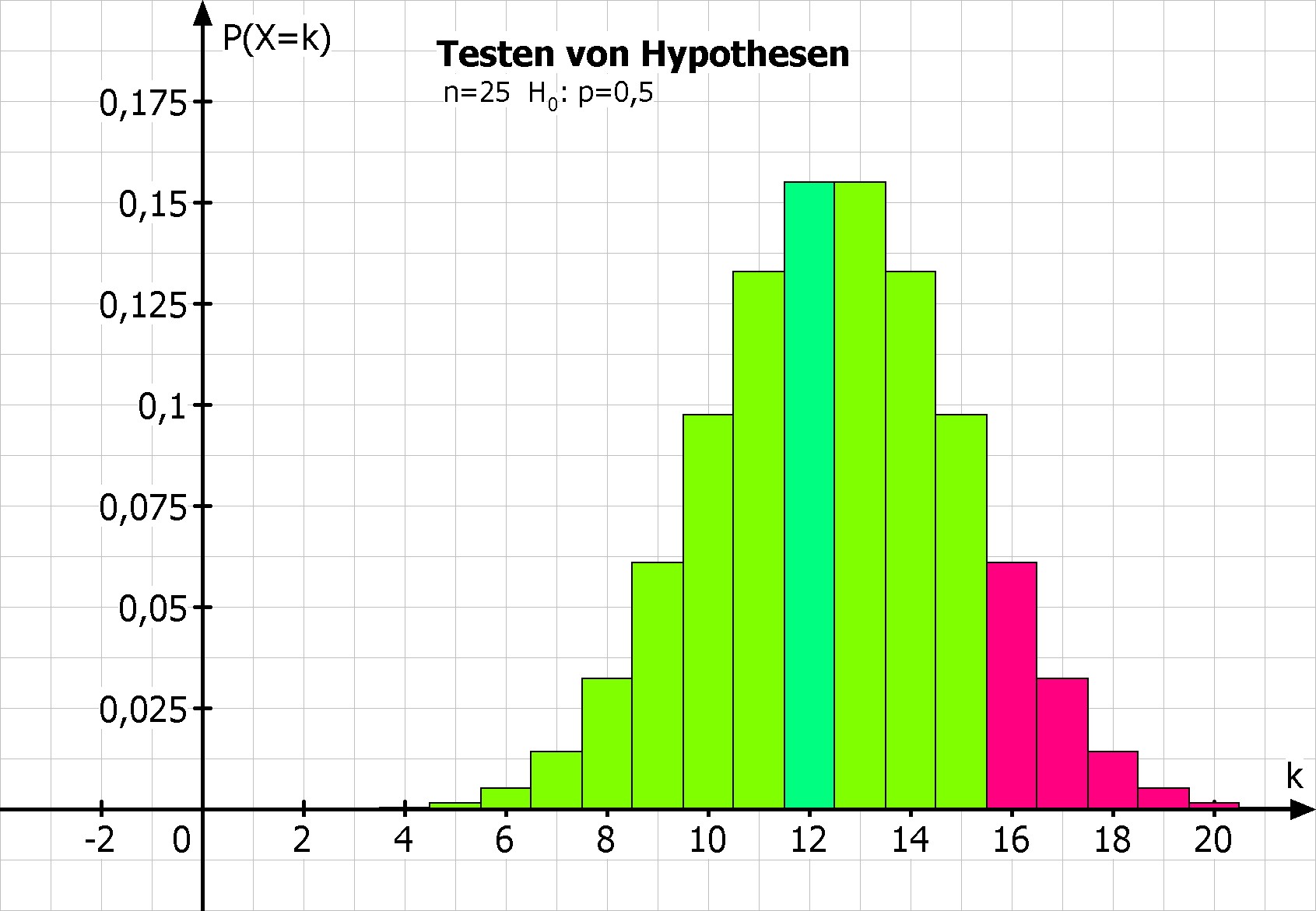    Bestimmung der zugehörigen Irrtumswahrscheinlichkeit α: Es gilt P(X≥16) = 1-P(X≤15) ≤ α.
    MatheGrafix liefert den exakten Wert α = 11,48%.
    
    Bild: Diese Darstellung erhält man unter dem Reiter "Binomial.", hierfür benötigt man nicht(!) das Modul "Testen".
    Im Rechenmodul wählt man unter dem Reiter "Binomialverteilung" den Bereich X≥16 aus und liest die Wahrscheinlichkeit 11,48% ab.
    Die Näherung erhält man ohne weitere Eingaben mit einem Wechsel auf den Reiter "Näherungsformel von de Moivre-Laplace" und liest hier die Wahrscheinlichkeit 11,51% ab. Da bei beiden Methoden der Ablehnungsbereich gleich bleibt, benötigt man zur Darstellung kein weiteres Bild.
    
    
  • Methode 2: Lösung mit der Näherungsformel von de Moivre-Laplace
    
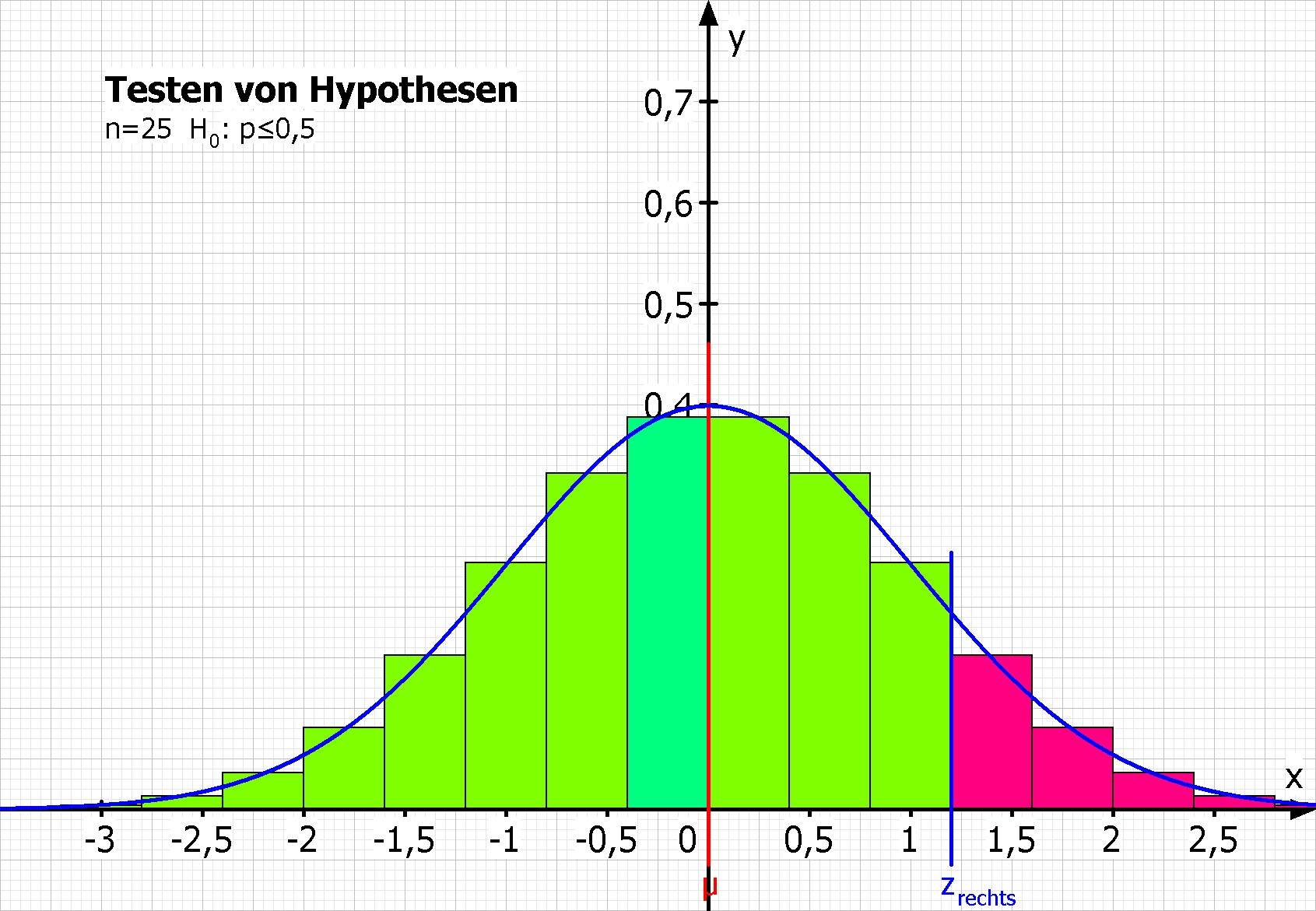    Man berechnet die summierte Wahrscheinlichkeit mit P(X≥16) = 1-P(X≤15) = 1-Φ(1,20) = 0,1151.
    MatheGrafix liefert mit dieser Methode α = 11,51%.
    
    Bild: Diese Darstellung erhält man unter dem Reiter "Näherungsformel von de Moivre-Laplace", indem man im Feld "Was wird gezeichnet?" ein Häkchen bei "Normalverteilung" und "standardisiert" setzt: Hier kann man den transformierten Wert z_rechts = 1,20 ablesen, der die Bereiche trennt und in der Rechnung 1-Φ(1,20) zu finden ist.

Ergebnis: Werden bei 25 Fragen mehr als 15 richtig beantwortet, kann H₀ abgelehnt werden: Die Vermutung bzw. Hypothese wird also abgelehnt, dass die Antworten geraten sind!
Mit einer Wahrscheinlichkeit von etwa 11,48% (bzw. 11,51% mit Näherung) ist dabei eine Fehlentscheidung möglich.

Download MatheGrafix-Dateien

Lösung: Ablehnungsbereich Binomialverteilung
Lösung: Standardisierte Binomialverteilung

Download Webseite als Word-Text

Testen von Hypothesen: Aufgaben und Lösungen