MatheGrafix 12 / Online-Hilfe

Aufgabe: Beidseitiger Test, Berechnung des Ablehnungsbereichs

Beim Münzwurf geht man davon aus, dass beide Ereignisse Wappen und Zahl gleichwahrscheinlich sind mit der Trefferwahrscheinlichkeit p = 0,5 für Wappen. Zur Überprüfung soll eine Münze nun 33-mal geworfen werden, wobei das Signifikanzniveau auf 5% festgelegt wird.

Lösung

Bestimmung des Ablehnungsbereichs mit den Tabellen der Binomialverteilung und mit der Näherungsformel von de Moivre-Laplace:

• Stichprobenumfang: n = 33
• Treffer bedeutet: Wappen liegt oben.
• Zufallsgröße X: Anzahl der Treffer
• X ist bei wahrer Nullhypothese B_33;0,5-verteilt.
• Die Hypothesen lauten: H₀:p = 0,5 (Die Münze sei ideal) und H₁:p ≠ 0,5.
  Da große Werte und kleine Werte von X gegen H₀ sprechen, handelt es sich um einen beidseitigen Test.
• Vorgegebenes Signifikanzniveau: α = 5%
  
  
• Bestimmung des Ablehnungsbereichs:
  
  
  • Methode 1: Lösung mit den Tabellen der Binomialverteilung
    
    
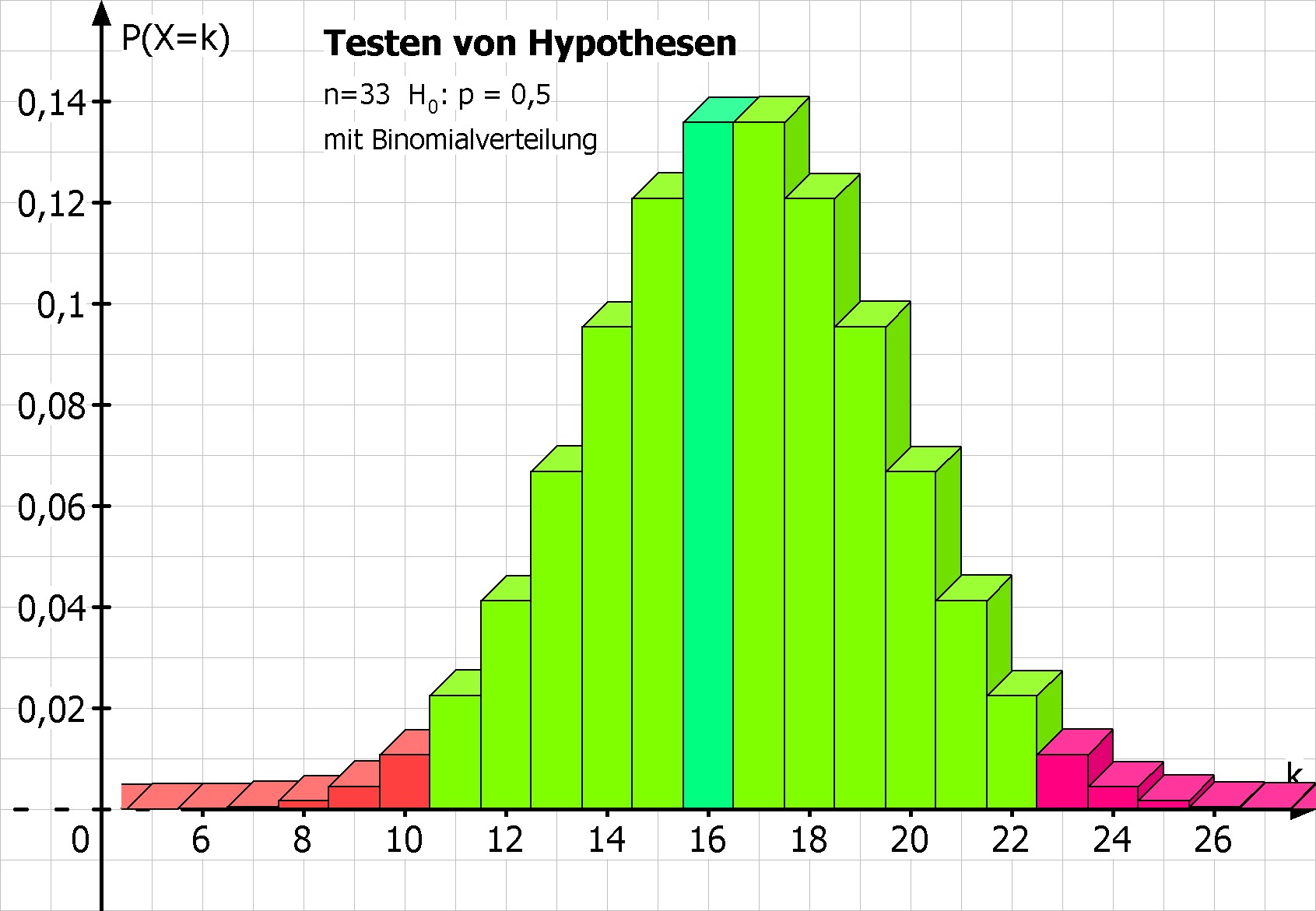
    Gesucht ist die kleinste Trefferzahl k mit P(X≥k) = 1-P(X≤k-1) ≤ 2,5% = α/2 und
    die größte Trefferzahl k mit P(X ≤ k) ≤ 2,5%% = α/2.
    MatheGrafix liefert den Ablehnungsbereich {0,...,10} ∪ {23,...,33}.
    Der genaue Wert für α ist bei dieser Methode 3,50%.
    
    Bild links: Diese Darstellung wird von MatheGrafix automatisch generiert. MatheGrafix berechnet den Ablehnungsbereich {0,...,10} ∪ {23,...,33}.
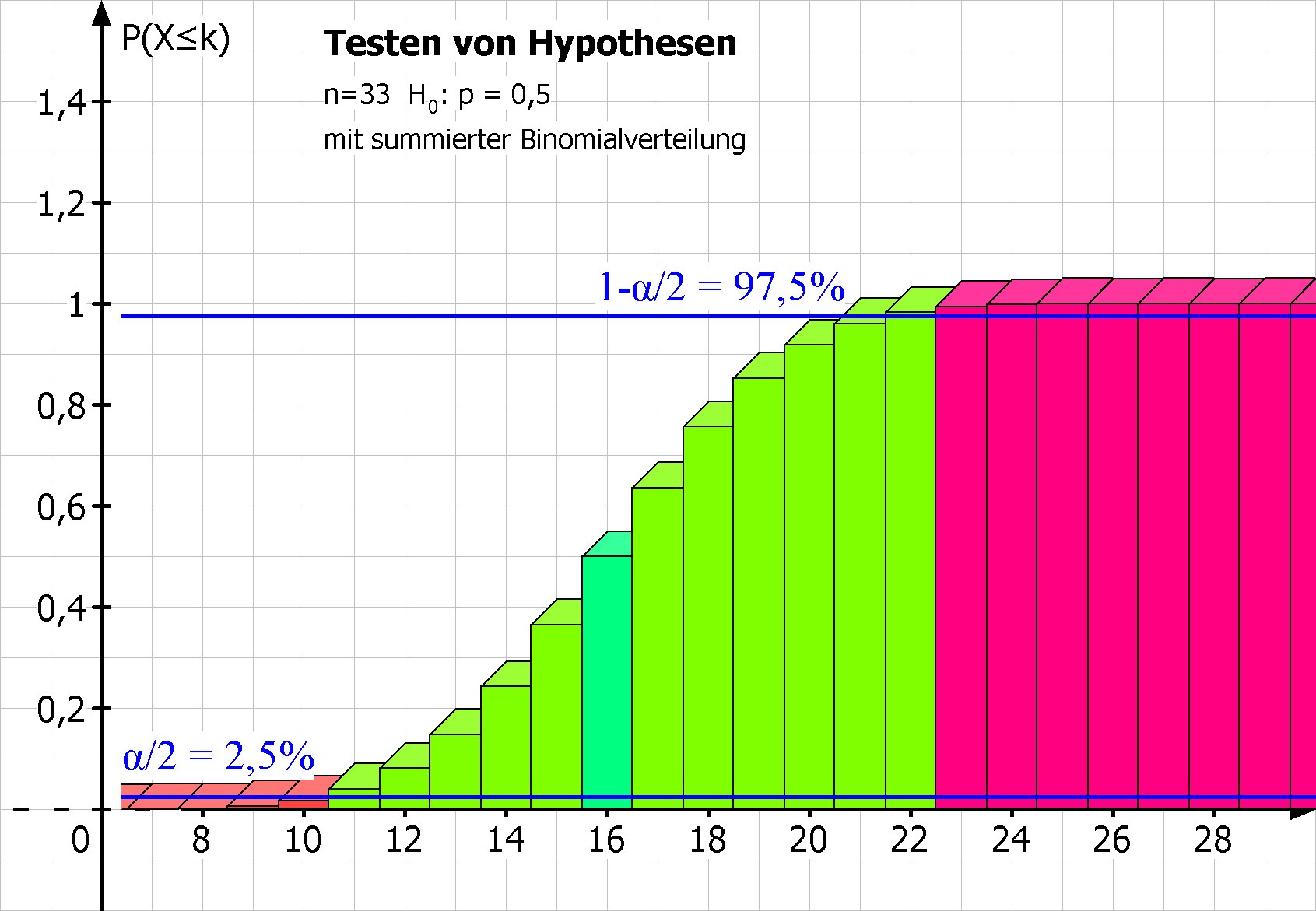
    Bild rechts: Bei der summierten Binomialverteilung wurden zwei Grenzen eingezeichnet:
    - die untere Grenze α=2,5% trennt den unteren Ablehnungsbereich vom Annahmebereich.
    - die obere Grenze 1-α=97,5% liefert wegen P(X≤k-1) ≥ 0,975 den Wert k-1=22, damit k=23 als untere Grenze für den oberen Ablehnungsbereich.
    
    
    
  • Methode 2: Lösung mit der Näherungsformel von de Moivre-Laplace
    
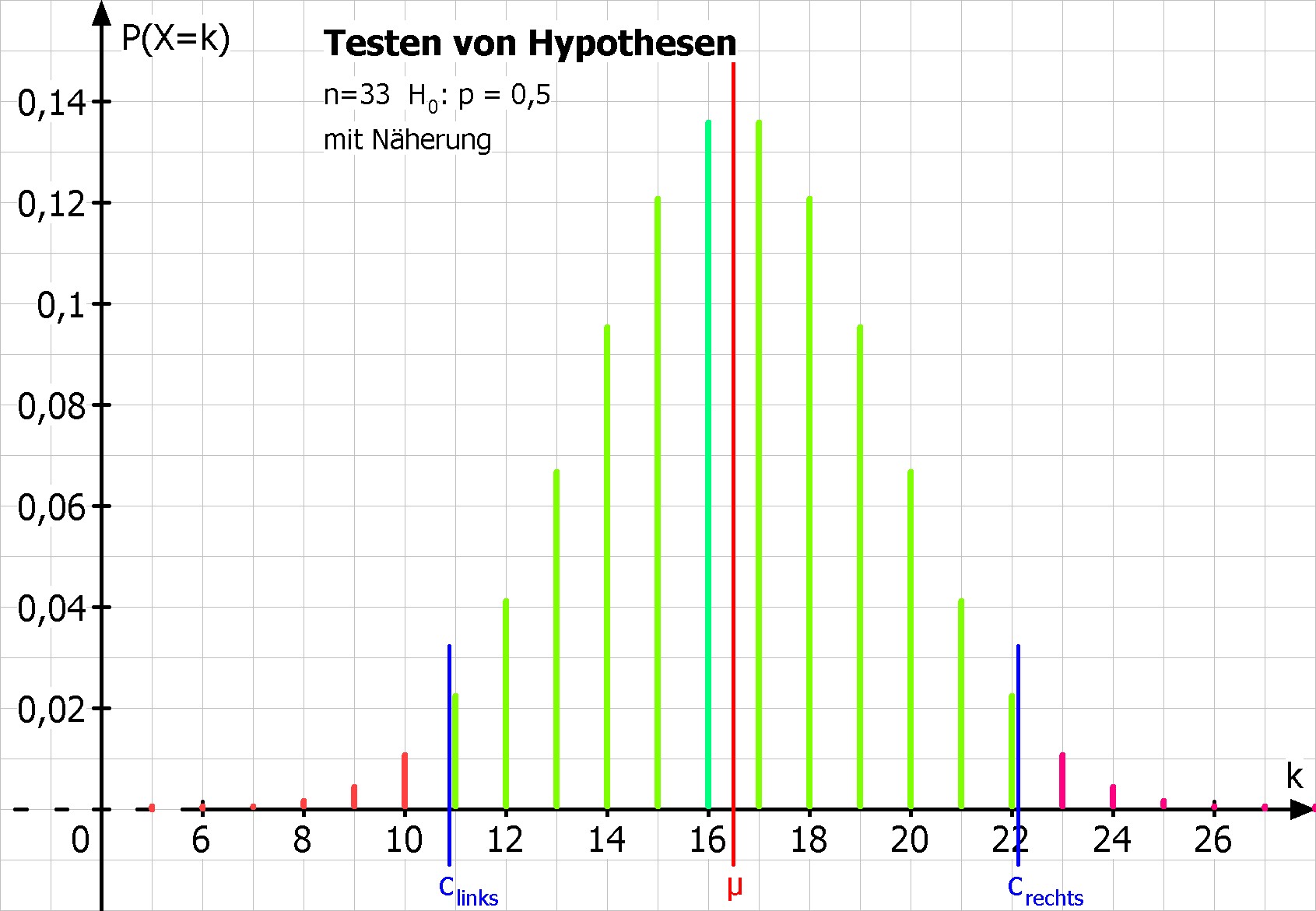    Man berechnet die Grenzen c_links = µ - 1,96*σ = 10,87 und c_rechts = µ + 1,96*σ = 22,13, diese trennen den Ablehnungsbereich vom Annahmebereich.
    MatheGrafix liefert mit dieser Methode ebenfalls den Ablehnungsbereich {0,...,10} ∪ {23,...,36}.
    
    Bild: Bei dieser Methode trennen die Senkrechten bei c_links und c_rechts den Ablehnungsbereich vom Annahmebereich. Die Darstellung mit Rechtecken oder Quadern eignet sich hier nicht, da die Trennung so nicht sichtbar wird. Daher wird die Binomialverteilung als Stabdiagramm dargestellt.

Ergebnis: Der Ablehnungsbereich von H₀ ist {0,...,10} ∪ {23,...,36}. Fallen bei 33 Würfen weniger als 11 oder mehr als 22-mal Wappen, kann mit einer Irrtumswahrscheinlichkeit von 5% abgelehnt werden, dass die Münze ideal ist.

Download MatheGrafix-Dateien

Lösung: Ablehnungsbereich Binomialverteilung
Lösung: Ablehnungsbereich summierte Binomialverteilung
Lösung: Ablehnungsbereich Näherungsformel

Download Webseite als Word-Text

Testen von Hypothesen: Aufgaben und Lösungen