MatheGrafix 12 / Online-Hilfe

Aufgabe: Linksseitiger Test, Fehler 1. und 2. Art

Der Vertreter einer Schuhmarke behauptet, dass mindestens 70 % aller Schuhgeschäfte die von ihm vertriebene Marke führen. Bei einer Überprüfung führen von 100 Schuhgeschäften allerdings nur 62 die Marke des Vertreters.

1. Lässt sich hieraus mit einer Irrtumswahrscheinlichkeit von höchstens 10% ein Widerspruch gegen die Behauptung des Vertreters herleiten?
2. Mit welcher Wahrscheinlichkeit wird die Behauptung des Vertreters fälschlicherweise angenommen, wenn in Wirklichkeit nur 60 % aller Schuhgeschäfte die von ihm vertriebene Marke führen (Fehler 2. Art)?

Lösung

a. Lösung

Bestimmung des Ablehnungsbereichs mit den Tabellen der Binomialverteilung und mit der Näherungsformel von de Moivre-Laplace:

• Stichprobenumfang: n = 100
• Ein Treffer bedeutet: Das Schuhgeschäft führt die Marke des Vertreters.
• Anzahl der Treffer in der Stichprobe: 62
• Zufallsgröße X: Anzahl der Treffer
• X ist bei wahrer Nullhypothese B_100;0,7-verteilt.
• Die Hypothesen lauten: H₀:p ≥ 0,7 (Die Behauptung des Vertreters sei wahr) und H₁:p < 0,7.
  Da kleine Werte von X gegen H₀ sprechen, handelt es sich um einen linksseitigen Test.
• Vorgegebenes Signifikanzniveau: α = 10%
  
  
• Bestimmung des Ablehnungsbereichs:
  
  
  • Methode 1: Lösung mit den Tabellen der Binomialverteilung
    
    
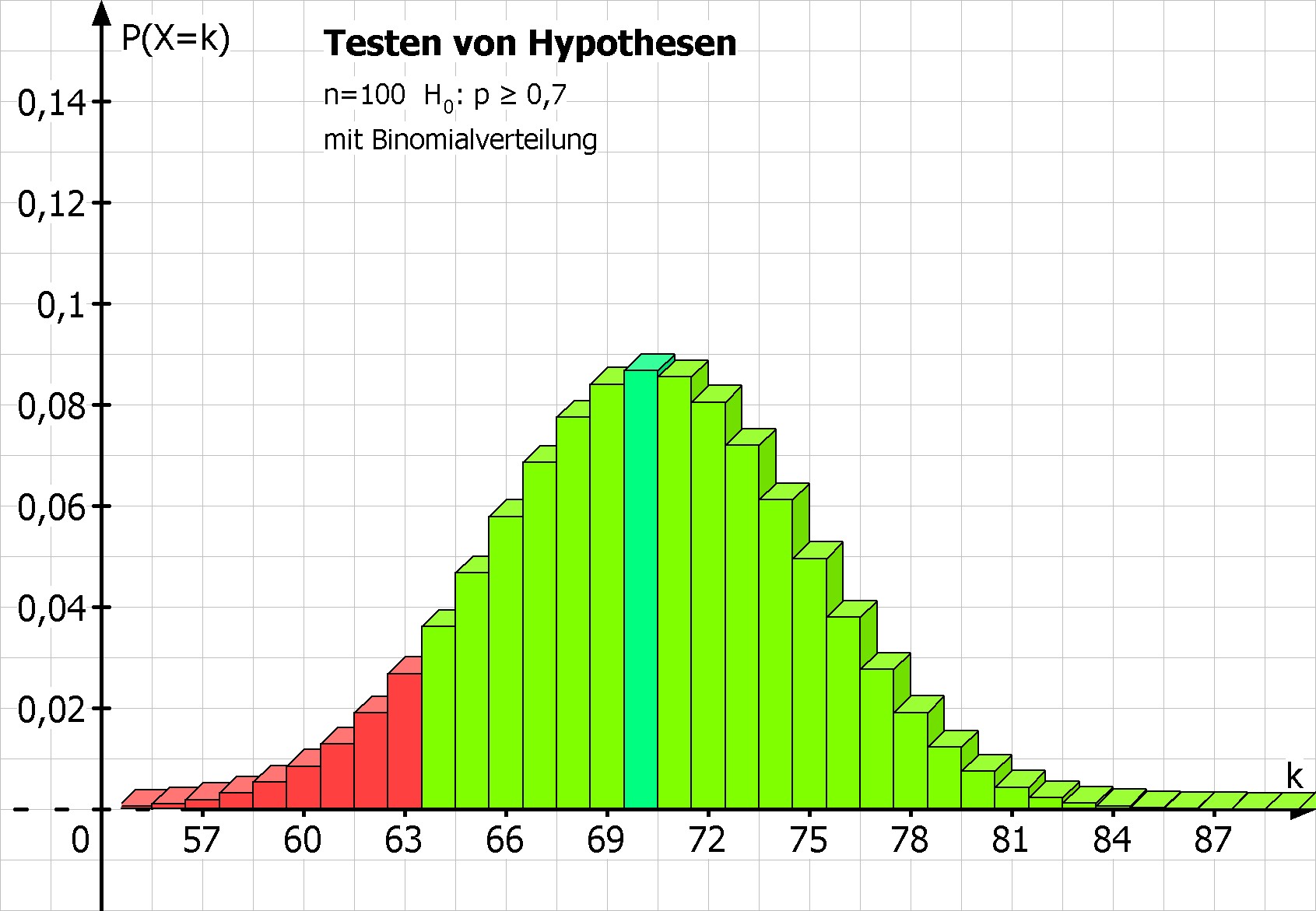
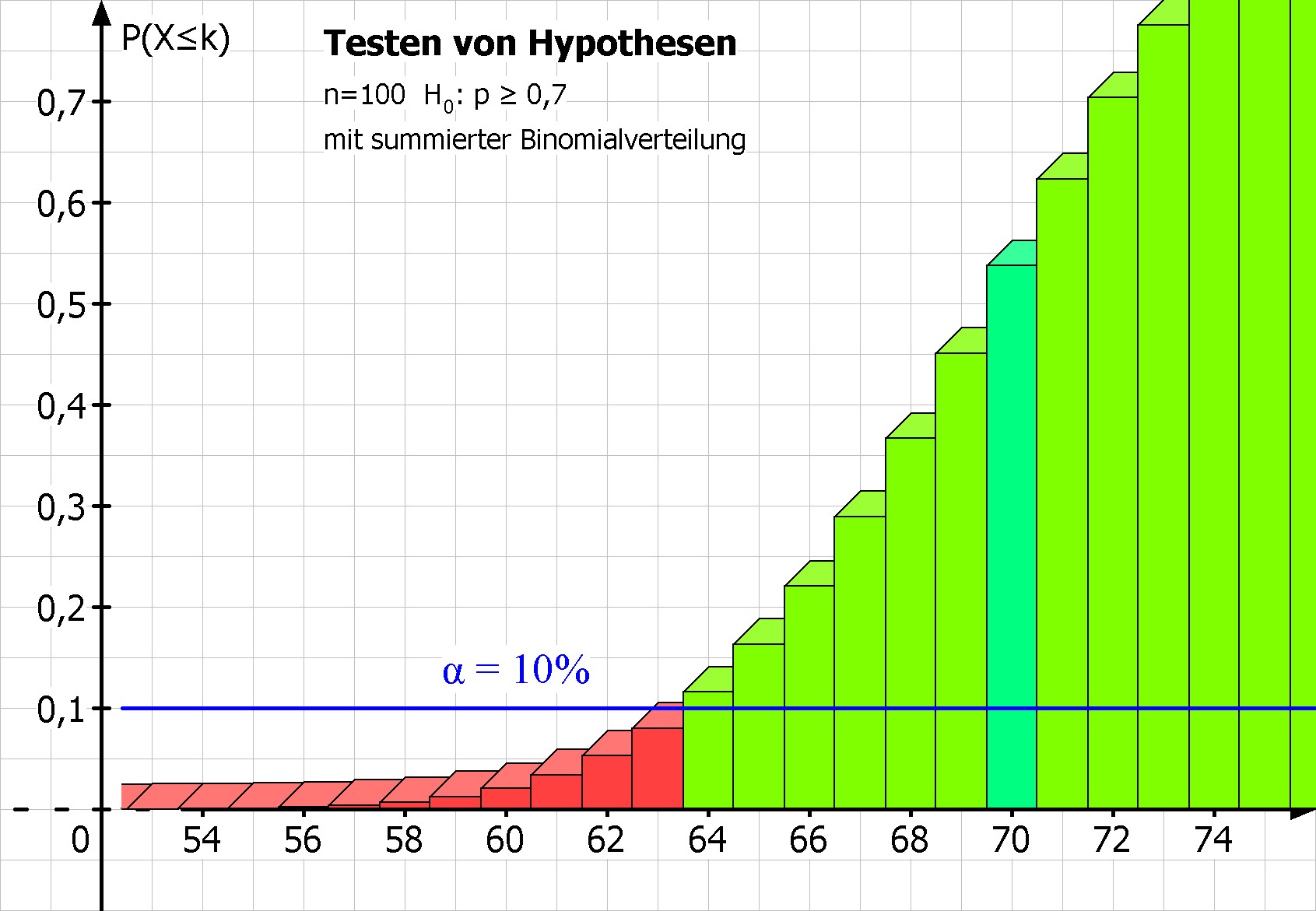
    Gesucht ist die größte Trefferzahl k mit P(X ≤ k) ≤ 10% = α.
    MatheGrafix liefert den Ablehnungsbereich {0,1,...,63}.
    Der genaue Wert für α ist bei dieser Methode 7,99%.
    
    Bild links: Diese Darstellung wird von MatheGrafix automatisch generiert. MatheGrafix berechnet den Ablehnungsbereich von 0 bis 63.
    Bild rechts: Bei der summierten Binomialverteilung wurde die Grenze α=10% eingezeichnet, die deutlich den Ablehnungsbereich von 0 bis 63 festlegt.
    
    
  • Methode 2: Lösung mit der Näherungsformel von de Moivre-Laplace
    
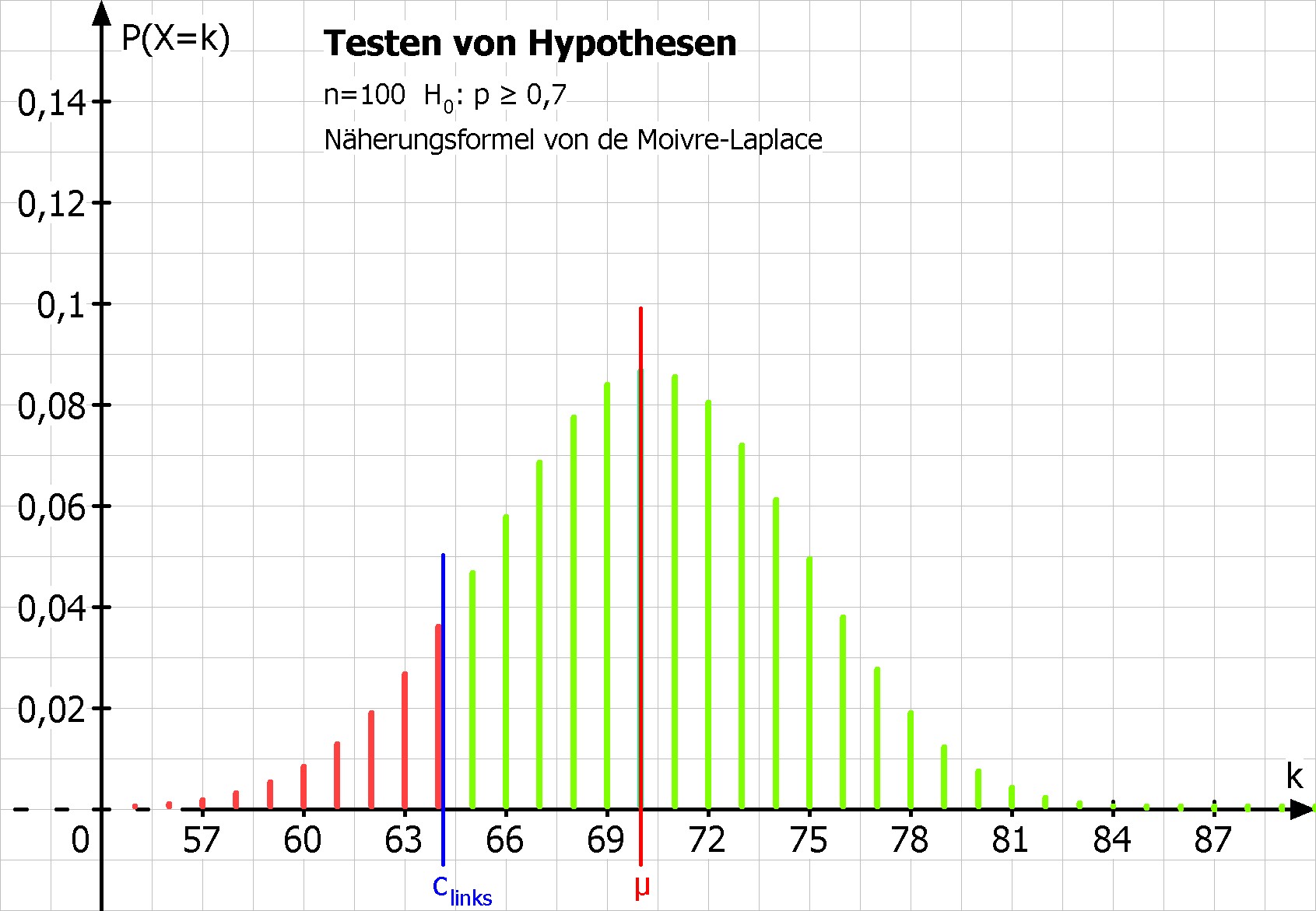    Man berechnet die Grenze c_links = µ - 1,28*σ = 64,13, diese trennt den Ablehnungsbereich und den Annahmebereich.
    MatheGrafix liefert mit dieser Methode den etwas größeren Ablehnungsbereich {0,1,...,64}.
    Der genaue Wert für α ist hier 11,61%.
    
    Bild: Bei dieser Methode trennt die Senkrechte bei c_links den Ablehnungsbereich und den Annahmebereich. Die Darstellung mit Rechtecken oder Quadern eignet sich hier nicht, da die Trennung so nicht sichtbar wird. Daher wird die Binomialverteilung als Stabdiagramm dargestellt.

Ergebnis: Da 62 bei beiden Methoden im Ablehnungsbereich liegt, wird H₀ verworfen. Mit einer Irrtumswahrscheinlichkeit von höchstens 10% lässt sich ein Widerspruch zur Behauptung des Vertreters herleiten.

b. Lösung

Bestimmung des Fehlers 2. Art mit den Tabellen der Binomialverteilung und mit der Näherungsformel von de Moivre-Laplace:

• Stichprobenumfang: n = 100
• Ein Treffer bedeutet: Das Schuhgeschäft führt die Marke des Vertreters.
• Zufallsgröße X': Anzahl der Treffer
• Die tatsächliche Trefferwahrscheinlichkeit beträgt p' = 0,6.
• X' ist dann B_100;0,6-verteilt.
• Bestimmung des Fehlers 2. Art:
  
  Bild
  Auch diese Darstellung wird von MatheGrafix automatisch generiert. MatheGrafix berechnet ebenfalls den Fehler 2. Art nach der gewünschten Methode (mit Hilfe der Tabelle der Binomialverteilung oder mit Hilfe der Näherungsmethode).
  Die alternative Verteilung zu p=0,6 wird kariert dargestellt und über die ursprüngliche Verteilung gelegt.
  Der für den Fehler 2. Art zu berechnende Bereich ist gelb kariert und entspricht dem Annahmebereich der ursprünglichen Verteilung mit p=0,7.
  
  
  • Methode 1: Lösung mit den Tabellen der Binomialverteilung
    Mit p' = 0,6 gilt für den Fehler 2. Art: β = P(X' ∊ Annahmebereich) = P(X' ≥ 64) = 23,86%.
    
  • Methode 2: Lösung mit der Näherungsformel von de Moivre-Laplace
    Mit p' = 0,6 gilt für den Fehler 2. Art: β = P(X' ∊ Annahmebereich) = P(X' ≥ 65) = 17,88% (Anzeige von "binomial" auf "Näherung" umgestellt!).

Ergebnis: Der Fehler zweiter Art beträgt β ≈ 24% nach dem Verfahren mit den Tabellen der Binomialverteilung, β ≈ 18% mit dem Näherungsverfahren. Die Behauptung des Vertreters wird mit einer Wahrscheinlichkeit von etwa 24% (18%) fälschlicherweise angenommen.

Download MatheGrafix-Dateien

Lösung a: Ablehnungsbereich Binomialverteilung
Lösung a: Ablehnungsbereich summierte Binomialverteilung
Lösung a: Ablehnungsbereich Näherungsformel
Lösung b: Binomialverteilung, Fehler 2. Art

Download Webseite als Word-Text

Testen von Hypothesen: Aufgaben und Lösungen