MatheGrafix 12 / Online-Hilfe

I. Die Funktionenschar einer Formel - Wurfparabeln und Hüllkurve

Die Funktionenschar von Wurfparabeln mit gemeinsamer Anfangsgeschwindigkeit wird für den Abwurfwinkel β von 5° bis 85° mit der Schrittweite 5° gezeichnet.
Mit einer weiteren Formel wird die Hüllkurve dieser Wurfparabeln gezeichnet.

I.1 Die Funktionenschar

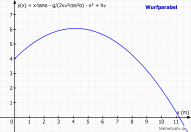
I.1.1 Eine Wurfparabel
In "Formel" unter "Beispiele" wird die "Wurfparabel"
y(x,β,v₀,h₀,g) = x∙tan(β) - g / (2∙v₀^2 ∙ cos(β)^2) ∙ x^2 + h₀
mit den Werten β=45°, v₀=9m/s, h₀=4m und g=9,81m/s² gezeichnet.

Anmerkung: Die Winkelfunktionen erlauben seit MatheGrafix 12 die Eingabe im Gradmaß nach der Umschaltung von Rad [R] in Deg [D].


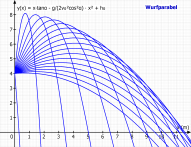
I.1.2 Die Wurfparabelschar
Durch das Umschalten des Reiters "Formel" auf den Reiter "Funktion" erhält man unmittelbar eine Funktionenschar dieser Formel:
- Beim Umschalten wird nur der erste Parameter geändert, für y(x,β,v₀,h₀,g) also β, alle anderen Parameter und der Definitionsbereich ändern sich nicht.
- Jetzt ändert man noch den Bereich von β in β von [5] bis [85] Schritt [5].
- Um die Wurfparabeln vollständig darzustellen vergrößert man die Höhe der y-Achse auf 10cm..

I.2 Die Hüllkurve

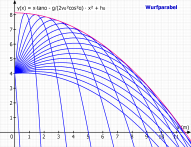
Die Formel der Hüllkurve nach Wikipedia ist dann in MatheGrafix
y(x,v₀,h₀,g) = -g / (2∙v₀^2) ∙ x^2 + v₀^2 / (2∙g) + h₀
oder ohne Sonderzeichen
y(x,v0,h0,g)= -g / (2*v0^2) * x^2 + v0^2 / (2*g) + h0 .

I.2.1 Erste Möglichkeit
- Im Modul "Funktion" wählt man die [2.] Funktion.
- Dann schaltet man zum Modul "Formel" um.
- Jetzt trägt man die Formel für die Hüllkurve ein.
- Danach ändert man noch die Parameter auf v₀=9m/s, h₀=4m und g=9,81m/s² und die Farbe der Hüllkurve auf Rot.

I.2.1 Zweite Möglichkeit
Die zweite Möglichkeit ist etwas übersichtlicher. Im linken Fenster wählt man unten im Feld "Bearbeiten" mit dem Button "Funktionen" den Funktionseditor aus:
- Unter 2. schaltet man ganz rechts mit dem Button xab auf das Formelmodul um.
- Jetzt trägt man unter 2. die Formel für die Hüllkurve ein.
- Nach dem Klick auf den Button "Parameter" ändert man noch die Parameter auf v₀=9m/s, h₀=4m und g=9,81m/s² und die Farbe der Hüllkurve auf Rot.

I.3 Schieberegler für Wurfparabel und Hüllkurve

Bisher haben wir den Schieberegler nicht vermisst, oder doch?
Die Wurfparabel, unsere 1. Funktion, haben wir ja unter Punkt 1.2 von "Formel" auf "Funktion" geschaltet und so die Kurvenschar erhalten.
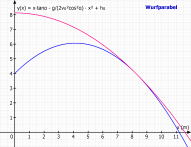
Nun schalten wir die 1. Funktion wieder von "Funktion" zu "Formel" und sehen natürlich nur noch eine Wurfparabel, die aber die Hüllfunktion berührt.
Jetzt können wir doch noch unseren Schieberegler für den Parameter β laufen lassen und sehen die Grenze, die von der Hüllkurve vorgegeben wird.

Hier ist das fertige Beispiel als MatheGrafix 12-Datei zum Downloaden.

---

II. Geradenschar und Hüllkurve

Dieses Beispiel ist in MatheGrafix integriert. Man findet es unter "Formel" im Feld "Beispiele" mit dem Button Geradenschar, Hüllkurve.

II.1 Die Hüllkurve

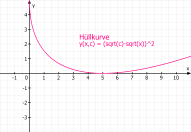In "Formel" unter "Beispiele" wird mit dem Button Geradenschar, Hüllkurve als [1.] Funktion die Hüllkurve y(x,c) = ( sqrt(c) - sqrt(x) ) ^2
mit dem Parameter c=5 gezeichnet.
Dieser Parameter c muss den gleichen Wert haben wie der Parameter c der Geradenschar.

II.2 Die Geradenschar

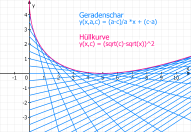Als [2.] Funktion wird unter dem Modul "Funktion" die Geradenschar
y(x,a,c) = (a-c)/a *x + (c-a)
mit a von [1} bis [15] Schritt [0,5] gezeichnet.
Den Parameter c findet man nach dem Umschalten von "Funktion" auf "Formel" mit c=5.

II.3 Der Schieberegler

Nach dem Umschalten der [2.] Funktion von "Funktion" auf "Formel" kann man auch den Schieberegler für den Parameter a laufen lassen und sieht die Grenze, die von der Hüllkurve vorgegeben wird.

Hier ist das Beispiel aus MatheGrafix 12 zusätzlich zum Downloaden.