MatheGrafix 12 / Online-Hilfe

Schieberegler, für jeden Parameter einer Formel

Mit Hilfe von Schiebereglern wird die Bedeutung von Parametern gezeigt, werden Aufgaben gelöst und werden physikalische Sachverhalte veranschaulicht.

1. Die Bedeutung der Parameter - Geradengleichung und Quadratische Funktion

1.1 Die Geradengleichung y = mx+b und die Bedeutung der Parameter m und b

Auf der Hilfeseite → Formel erstellen wird die Schreibweise y(x,m,b) = m*x + b in MatheGrafix erklärt.
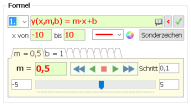Das Beispiel in MatheGrafix: Im Modul "Daten" unter dem Reiter "Beispiele" klickt man auf den Button "Geradengleichung", die Parameter m und b werden in die Tabelle übernommen.
Nun lässt man den Schieberegler für m automatisch laufen - mit dem einfachen Dreieck im Sekundentakt, mit dem doppelten Dreieck fünfmal schneller. Man sieht sofort:
Der Parameter m ist für die Steigung der Geraden verantwortlich.
Nach dem Wechsel zum Parameter b und dem automatischen Lauf des Schiebereglers sieht man:
Der Parameter b liefert den y-Achsenabschnitt der Geraden.

1.2 Die Parabelgleichung mit Linearfaktoren und die Bedeutung der Parameter a, x₁ und x₂

Die quadratische Gleichung mit Linearfaktoren f(x) = a(x-x₁)(x-x₂) schreibt man in MatheGrafix in der Form
f(x,a,x₁,x₂) = a∙(x-x₁)∙(x-x₂).
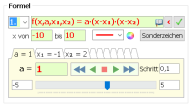Das Beispiel in MatheGrafix: Im Modul "Daten" unter dem Reiter "Beispiele" startet man mit einem Klick auf den Button "Quad. Fktn.: Linearfaktoren" das Beispiel, die Parameter a, x₁ und x₂ werden in die Tabelle übernommen.
Nun lässt man den Schieberegler für a automatisch laufen und sieht:
Der Parameter a ist für die Öffnung der Parabel verantwortlich, die Nullstellen x₁ und x₂ bleiben erhalten.
Nach dem automatischen Lauf des Schiebereglers für den Parameter x₁ ergibt sich:
Der Parameter x₁ ist für die Nullstelle x₁ verantwortlich, die Nullstelle x₂ und die Öffnung der Parabel bleiben erhalten.
Nach dem Wechsel zum Parameter x₂ ergibt sich entsprechend:
Der Parameter x₂ ist für die Nullstelle x₂ verantwortlich, die Nullstelle x₁ und die Öffnung der Parabel bleiben erhalten.

2. Lösen von Aufgaben - Optimaler Abstoßwinkel beim Kugelstoßen

Aufgabe: Ein Kugelstoßer stößt die Kugel mit einer Geschwindigkeit von 8 m/s aus einer Höhe von h₀ = 1,80 m. Ist der Abstoßwinkel 45° gegen die Horizontale der optimal Winkel für die größte Weite?

Etwas Theorie (die für die experimentelle Lösung der Aufgabe entbehrlich ist!):
Eine Eisenkugel beim Kugelstoßen bewegt sich nahezu parabelförmig, die Wurparabel kann mit der Funktion
y(x) = x∙tanα - g / (2v₀² cos²α) ∙ x² + h₀ dargestellt werden.
Die Schreibweise in MatheGrafix mit dem Winkel β im Gradmaß und den Winkelfunktionen im Bogenmaß ist
y(x,β,v₀,h₀,g) = x∙tan(β ∙π/180) - g / (2∙v₀^2 ∙ cos(β ∙π/180)^2) ∙ x^2 + h₀.

Neu in Version 12: Die Umstellung von Bogenmaß R zu Gradmaß D für die Winkelfunktionen erlaubt eine weitere Vereinfachung: Für Winkel β im Gradmaß schreibt man nach der Umstellung nur noch
y(x,β,v₀,h₀,g) = x∙tan(β) - g / (2∙v₀^2 ∙ cos(β)^2) ∙ x^2 + h₀.

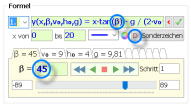Die experimentelle Lösung
Im Modul "Daten" unter dem Reiter "Beispiele" klickt man auf den Button "Wurfparabel", die Parameter β, v₀, h₀ und g werden in die Tabelle übernommen.
Bis auf β sind die Parameter bekannt und man trägt ein: v₀ = 8, h₀ = 1,80 und für g ist bereits 9,81 vorgegeben.
Gesucht ist ja der optimale Winkel β mit der maximalen Weite:
Man lässt den Schieberegler für β automatisch laufen - zunächst schnell mit dem doppelten Dreieck, dann mit dem einfachen Dreieck (mit langsamen Doppelklick) im Einzelschritt.
Ergebnis: Der optimale Winkel ist bei etwa 39° zu finden, bei 45° verschenkt er mehr als 10cm Weite.

3. Veranschaulichen physikalischer Sachverhalte - Schwebung und ANC

Physik: Wie entstehen Schwebungen? Zwei Töne ähnlicher Lautstärke mit leicht verschiedenen Frequenzen f1 und f2 treffen auf unser Ohr. Formal lässt sich der Sachverhalt als Überlagerung der Schwingungen zweier Schallquellen darstellen:
y(t) = y₁sin(2πf₁t) + y₂sin(2πf₂t).
Diese Formel schreibt man in MatheGrafix mit den Parametern auf der linken Seite der Gleichung in der Form
y(t,f1,f2,y1,y2) = y1*sin(2*π*f1*t) + y2*sin(2*π*f2*t).
Mit den neuen Sonderzeichen für "Mal" und tiefer gestellten Zahlen lässt sich die Formel übersichtlicher darstellen:
y(t,f₁,f₂,y₁,y₂) = y₁∙sin(2∙π∙f₁∙t) + y₂∙sin(2∙π∙f₂∙t).

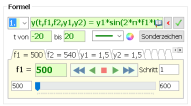Das Beispiel in MatheGrafix: Im Modul "Daten" unter dem Reiter "Beispiele" startet man mit einem Klick auf den Button "Akustische Schwebung" das Beispiel. Die Parameter f1, f2, y1, y2 werden in die Tabelle übernommen mit f1=500(Hz) und f2=540(Hz). Man sieht im rechten Fenster von MatheGrafix den
Graphen einer Schwebung als Überlagerung beider Schwingungen.
Lässt man nun den Schieberegler für die Frequenz f1 automatisch laufen, ändert sich die Frequenz f1 von 500(Hz) über 540(Hz) bis zu 600(Hz) und man sieht im rechten Fenster sehr deutlich das Verhalten der Schwebungsfrequenz.

Ausblick: Kehrt man die Amplitude der 2. Schwingung um, indem man in der Formel das + durch ein - ersetzt, erhält man ein Beispiel für Active Noise Cancellation (ANC). Dabei werden z.B. bei Bang & Olufsen zusätzliche geräuschunterdrückende Lautsprecher verwendet, um unerwünschte Hintergrundgeräusche zu reduzieren.
In MatheGrafix: Das unerwünschte Geräusch der zweiten Schwingung mit der Amplitude y2 und der Frequenz f2=540(Hz) wird durch die erste Schwingung bei f1=540(Hz) vollständig neutralisiert!