MatheGrafix 12 / Online-Hilfe

I. Aufgaben zur Standardnormalverteilung

Die Zufallsgröße Z ist standardnormalverteilt mit dem Erwartungswert µ=0 und der Standardabweichung σ=1.
Bestimme die Wahrscheinlichkeiten mit Hilfe der Tabelle der Verteilungsfunktion Φ(x) der Standardnormalverteilung:

1. P(Z ≤ -1,64)
2. P(Z ≥ 1,28)
3. P(-1,96 ≤ Z ≤ 1,96)

Lösung

Bestimmung der Wahrscheinlichkeiten mit Hilfe der in MatheGrafix integrierten Tabelle der Verteilungsfunktion der Standardnormalverteilung: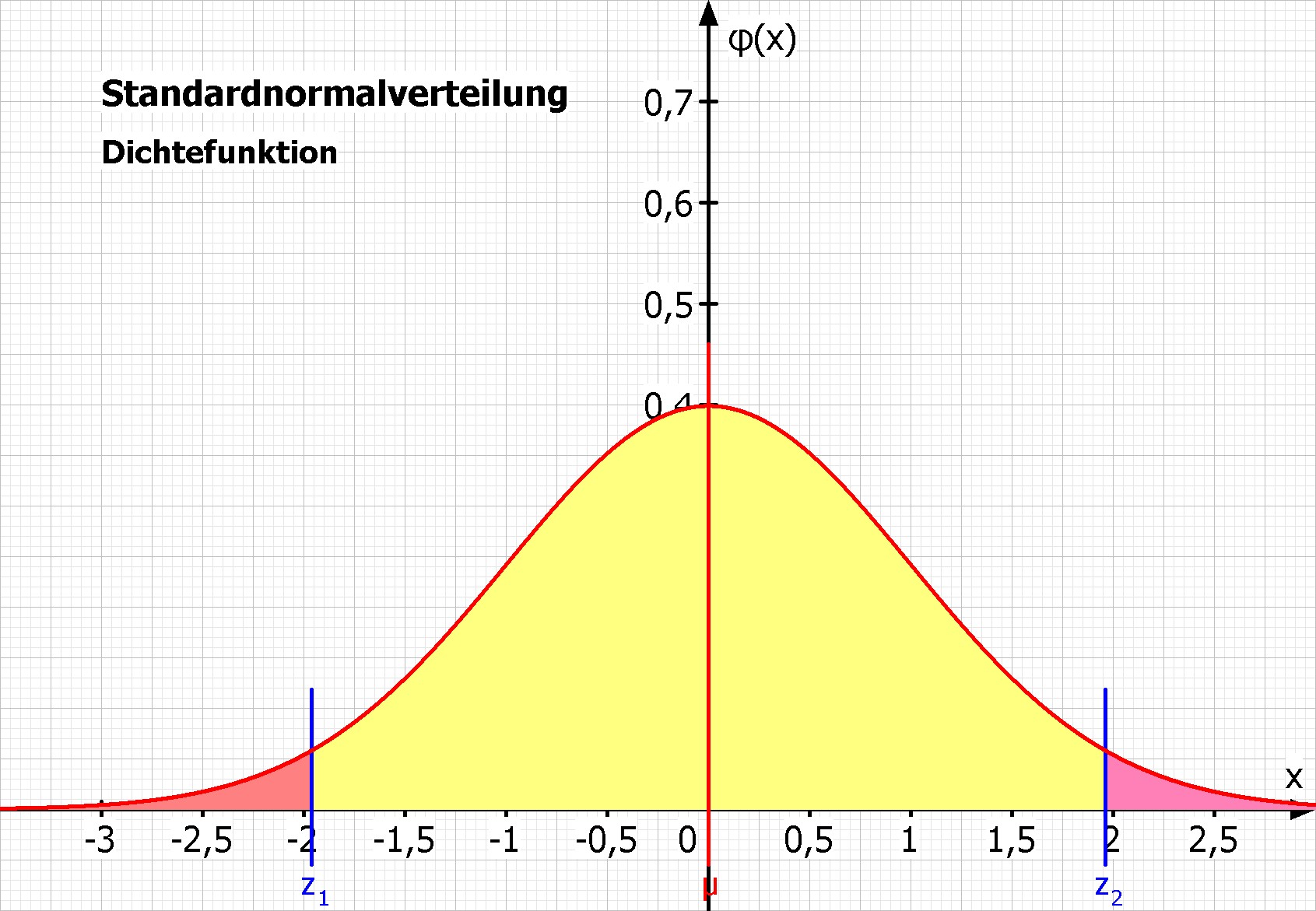

1. P(Z ≤ -1,64) = Φ(-1,64) = 5,05%
2. P(Z ≥ 1,28) = 1 - Φ(1,28) = 10,03%
3. P(-1,96 ≤ Z ≤ 1,96) = Φ(1,96) - Φ(-1,96) = 95,00%

Bilder: Links ist die Dichtefunktion φ(x) und rechts die Verteilungsfunktion Φ(x) der Standardnormalverteilung zu Teilaufgabe c.

Download MatheGrafix-Dateien

Lösung I.c: Standardnormalverteilung, Dichtefunktion
Lösung I.c: Standardnormalverteilung, Verteilungsfunktion

II. Aufgaben zur Normalverteilung mit µ=33,8 und σ=5,2

Die Zufallsgröße X ist normalverteilt mit dem Erwartungswert µ=33,8 und der Standardabweichung σ=5,2.
Bestimme die Wahrscheinlichkeiten mit Hilfe der Tabelle der Verteilungsfunktion Φ(x) der Standardnormalverteilung:

1. P(X ≤ 27,4)
2. P(X ≥ 38,1)
3. P(29,7 ≤ X ≤ 36,1)

Lösung

Bestimmung der Wahrscheinlichkeiten mit Hilfe der in MatheGrafix integrierten Tabelle der Verteilungsfunktion der Standardnormalverteilung: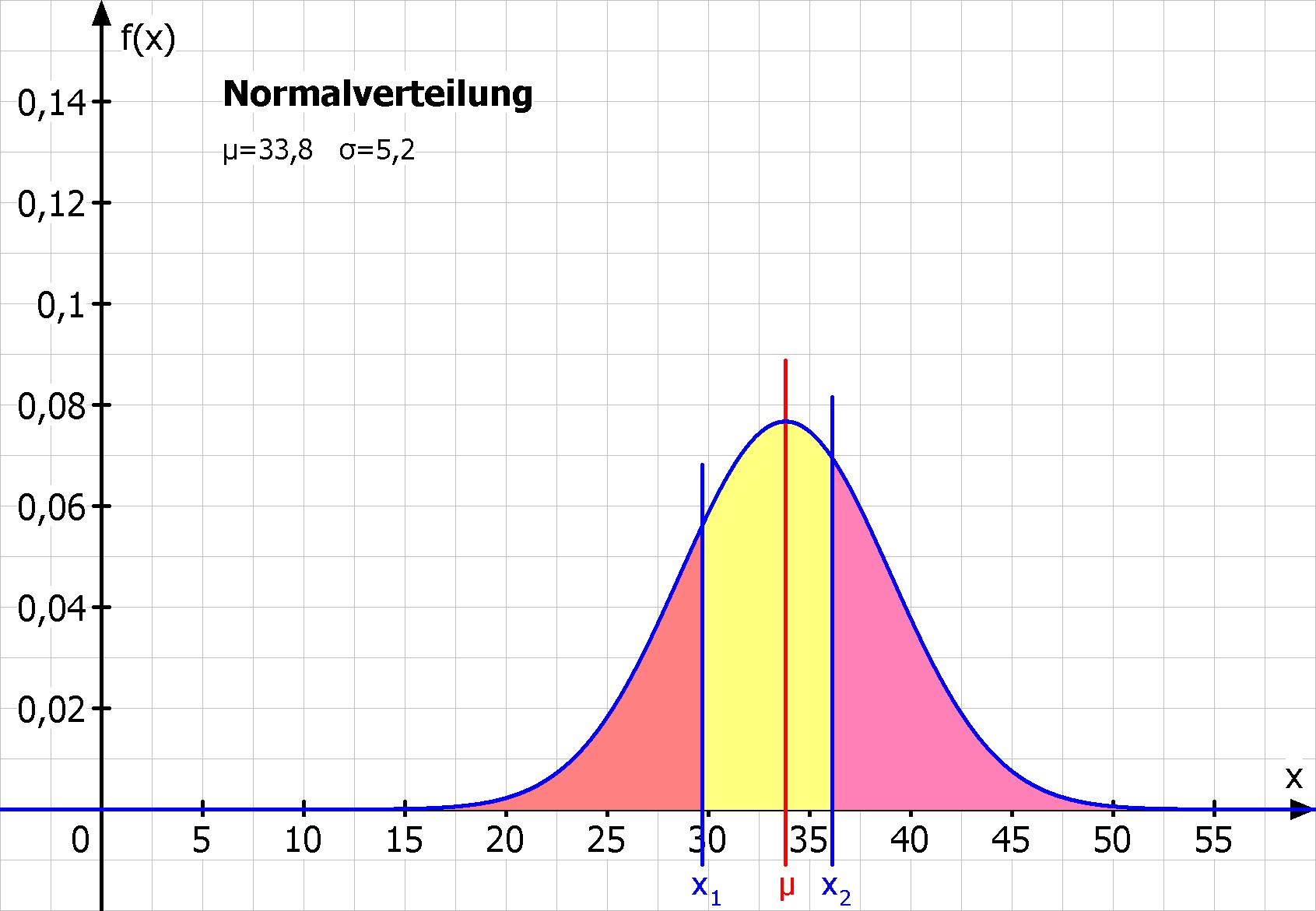

1. P(X ≤ 27,4) = Φ(-1,23) = 10,93%
2. P(X ≥ 38,1) = 1 - Φ(0,83) = 20,33%
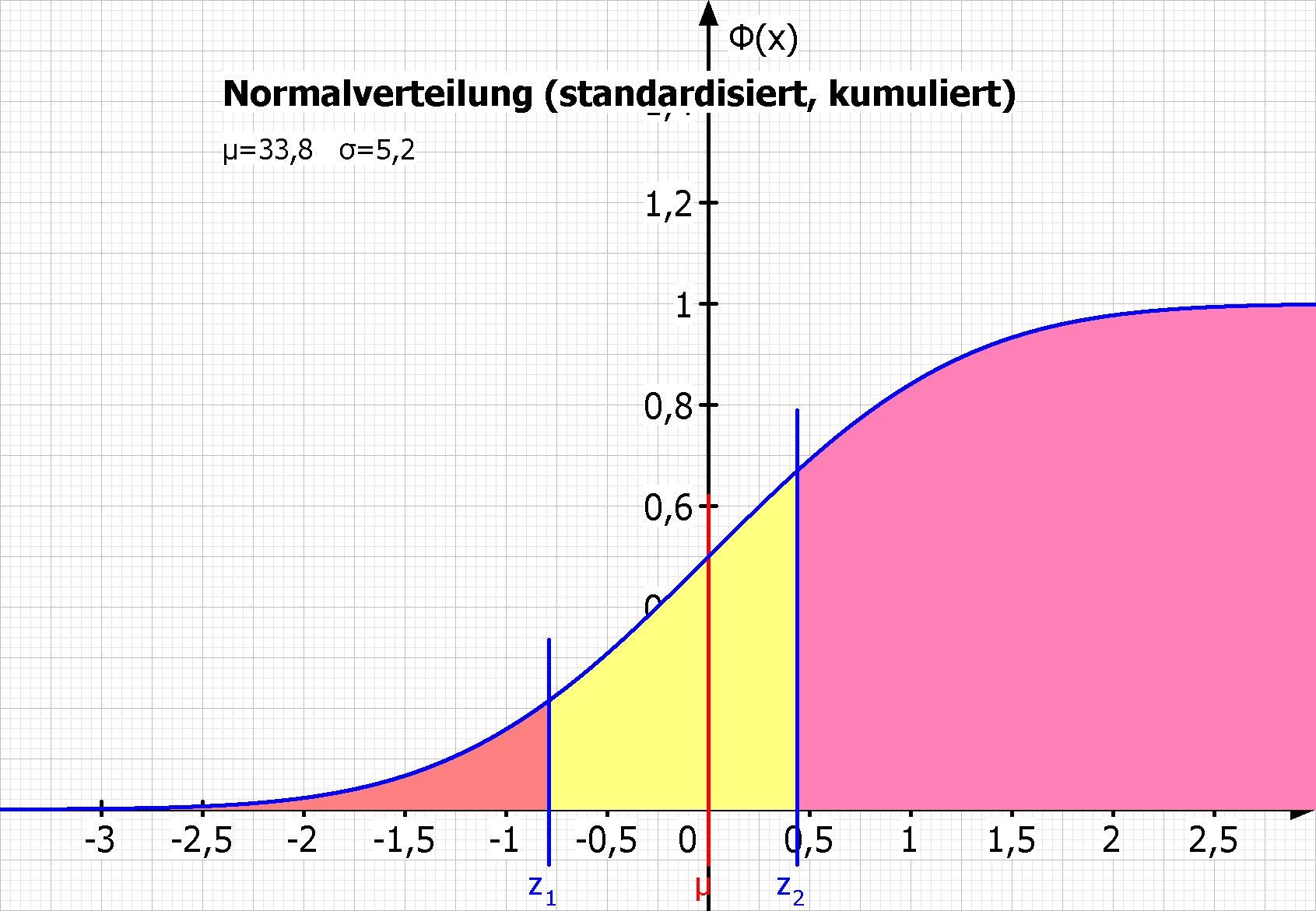
3. P(29,7 ≤ X ≤ 36,1) = Φ(0,44) - Φ(-0,79) = 45,52%

Bilder
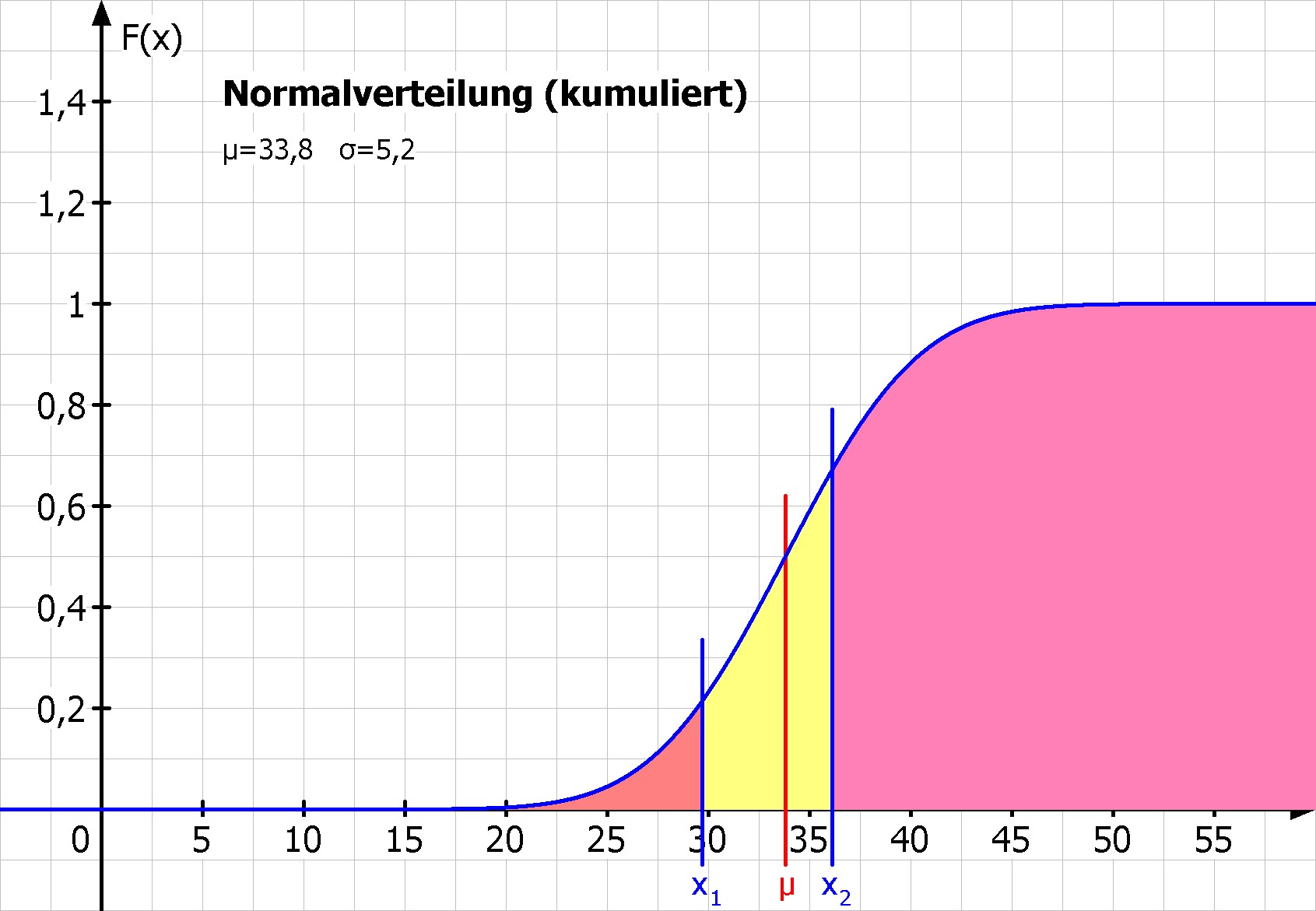
In der ersten Reihe sieht man links die Dichtefunktion und rechts die Verteilungsfunktion der Zufallsgröße X zu Teilaufgabe c.
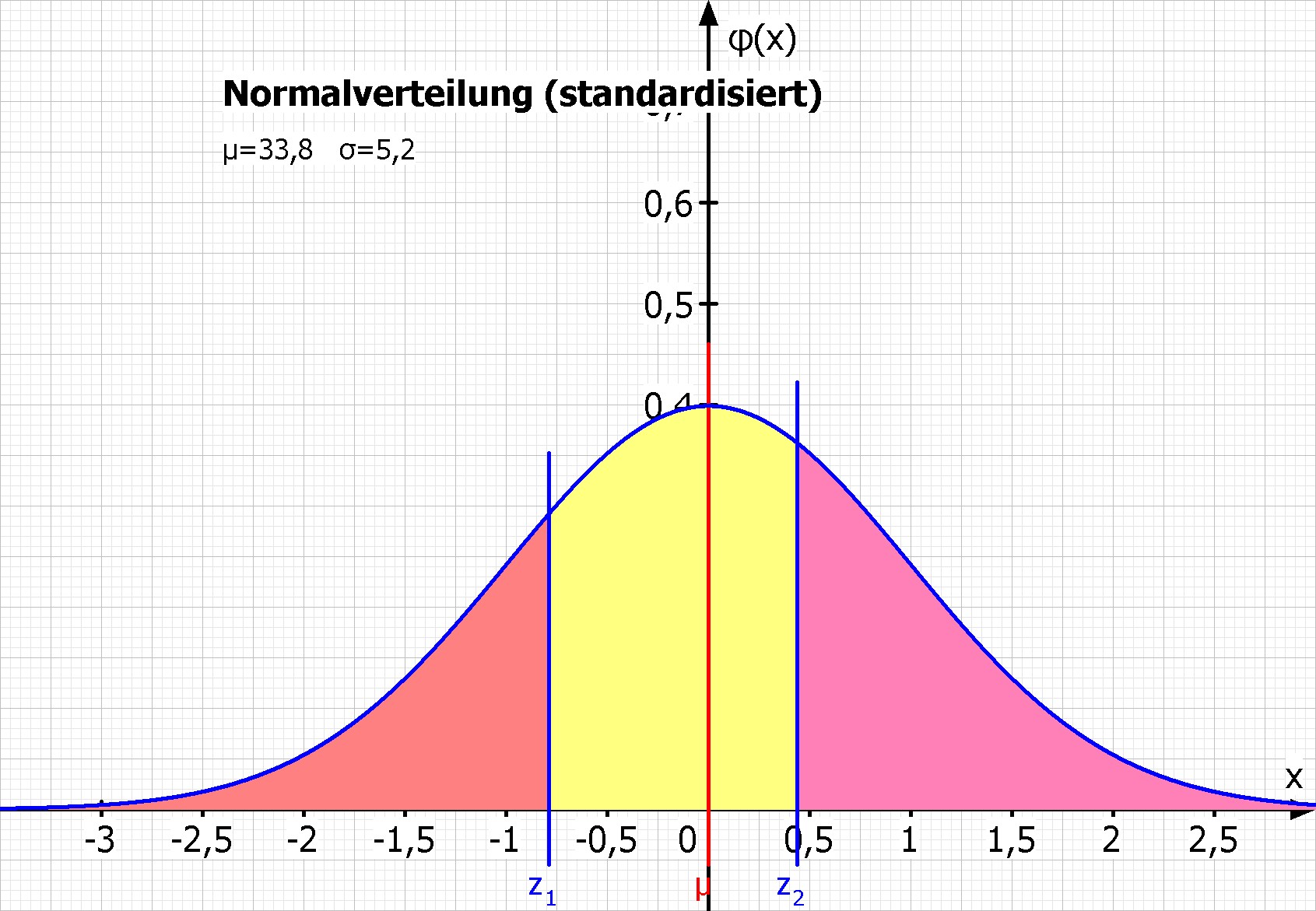
In der zweiten Reihe sind die Dichtefunktion und Verteilungsfunktion standardisiert. MatheGrafix transformiert automatisch die Werte x₁ = 29,7 und x₂ = 36,1 zu den Werten z₁ = -0,79 und z₂ = 0,44 und stellt sie als Senkrechte dar.

Download MatheGrafix-Dateien

Lösung II.c: Normalverteilung
Lösung II.c: Normalverteilung (kumuliert)
Lösung II.c: Normalverteilung (standardisiert)
Lösung II.c: Normalverteilung (standardisiert, kumuliert)

Download Webseite als Word-Text

Verteilungen: Aufgaben und Lösungen