MatheGrafix 12 / Online-Hilfe

I. Aufgaben zur Binomialverteilung mit Tabellen

Eine Zufallsgröße X ist B_20;1/3-verteilt, also binomialverteilt mit n=20 und p=1/3.
Berechne die Wahrscheinlichkeiten mit Hilfe der Tabelle der summierten Binomialverteilung für n=20 und p=1/3:

1. P(X ≤ 4)
2. P(X ≥ 7)
3. P(3 ≤ X ≤ 11)
4. P(X > 10)
5. P(5 ≤ X < 8)
6. P(4 < X < 16)
7. P(X = 7)

Lösung

Berechnung der Wahrscheinlichkeiten mit Hilfe der in MatheGrafix integrierten Tabellen der summierten Binomialverteilung:
Die Aufgaben a bis f können direkt abgelesen werden, die Aufgaben d bis g werden angepasst, dann abgelesen:

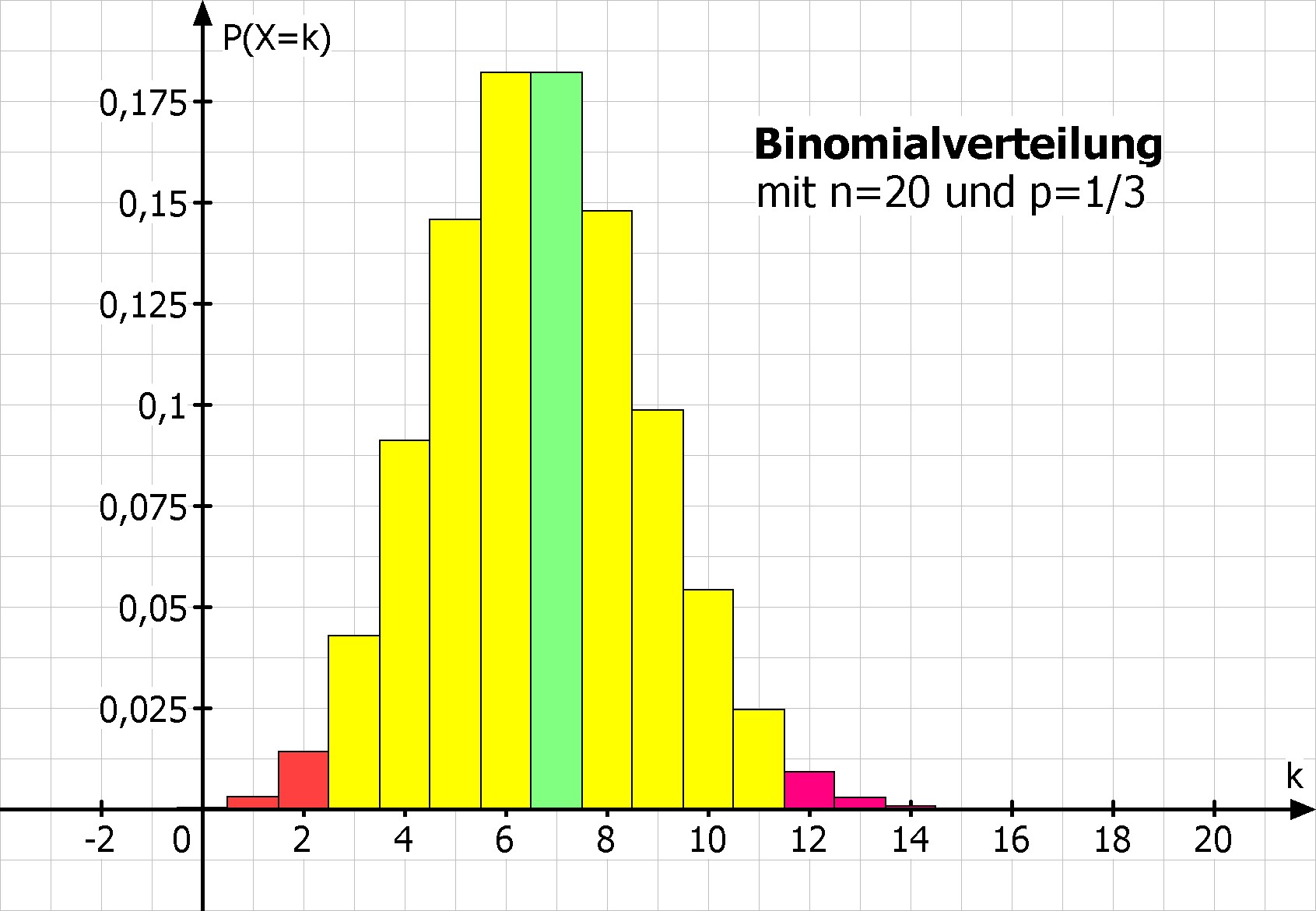
1. P(X ≤ 4) = 15,15%
2. P(X ≥ 7) = 52,07%
3. P(3 ≤ X ≤ 11) = 96,94%
4. P(X > 10) = P(X ≥ 11) = 3,76%
5. P(5 ≤ X < 8) = P(5 ≤ X ≤ 7) = 51,0%
6. P(4 < X < 16) = P(5 ≤ X ≤ 15) = 84,85%
7. P(X = 7) = P(7 ≤ X ≤ 7) = 18,22%

Bild: Das Histogramm zeigt Teilaufgabe c.




Sehr oft gibt es Aufgaben zur Binomialverteilung mit einer Anzahl n oder einer Wahrscheinlichkeit p, zu denen in den Formelsammlungen keine Tabellen zu finden sind. Hier benutzt man die Näherungsformel von de Moivre-Laplace, jeweils mit oder ohne Stetigkeitskorrektur von 0,5, wenn die Faustformel n*p*(1-p)>9 erfüllt ist.
In MatheGrafix können diese Aufgaben zusätzlich auch für sehr große n und beliebigen Wahrscheinlichkeiten p mit den Tabellenwerten der Binomialverteilung gelöst werden.

II. Aufgaben zur Binomialverteilung mit der Näherungsformel von de Moivre-Laplace

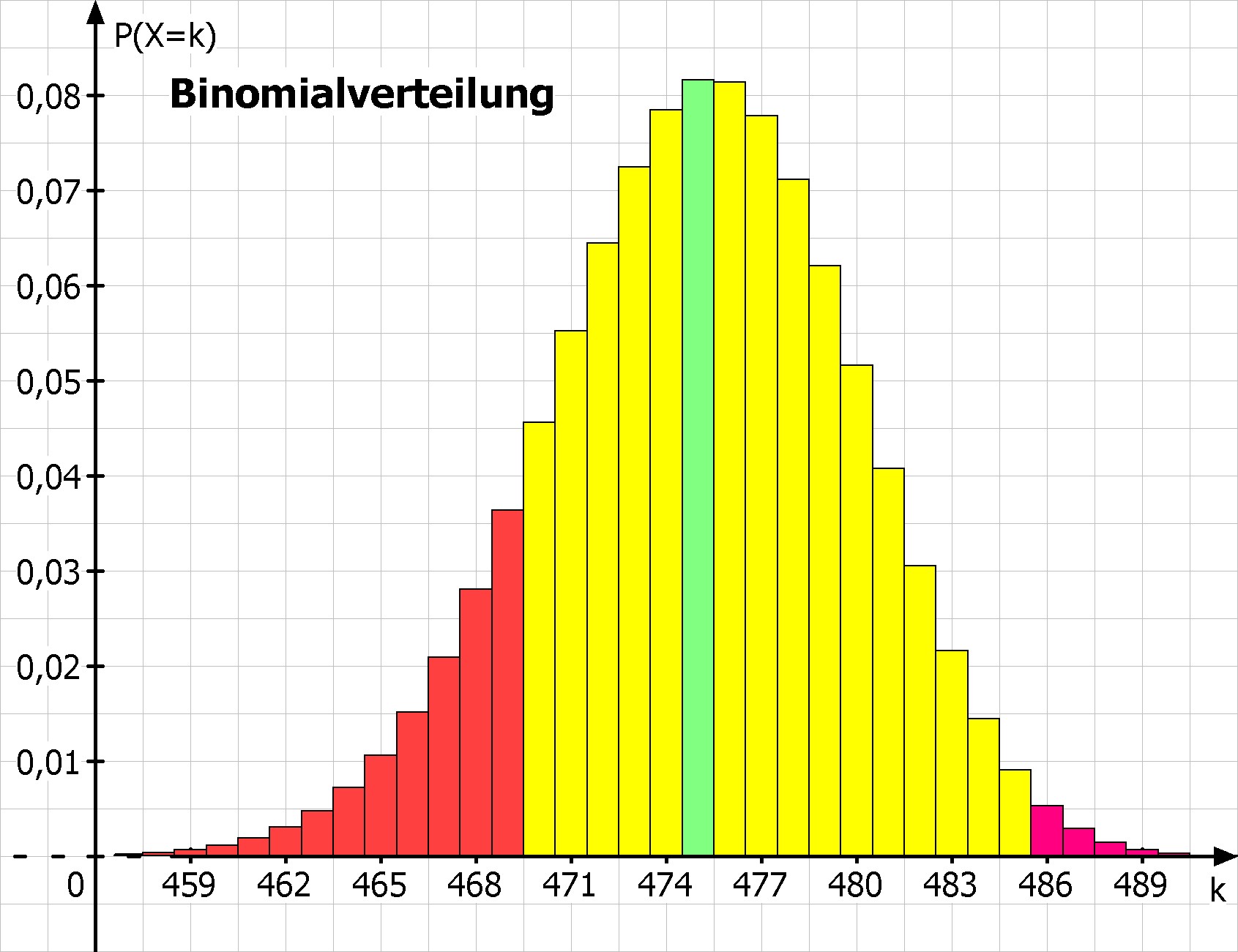
Eine Zufallsgröße X ist B_500;0,95-verteilt, also binomialverteilt mit n=500 und p=95%.
Berechne die Wahrscheinlichkeiten mit Hilfe der Tabelle der Näherungsformel von de Moivre-Laplace:

1. P(X ≤ 470)
2. P(X ≥ 480)
3. P(470 ≤ X ≤ 485)

Lösung

Berechnung der Wahrscheinlichkeiten mit Hilfe der in MatheGrafix integrierten Näherungsformel von de Moivre-Laplace:
Berechneter Mittelwert µ = n*p = 475, berechnete Standardabweichung σ = √(n*p*q) = √23,75 = 4,8734

1. ohne Korrektur: P(X ≤ 470) = Φ((470-475)/√23,75) ≈ Φ(-1,03) = 15,15%
   mit Korrektur: P(X ≤ 470) = Φ((470+0,5-475)/√23,75) ≈ Φ(-0,92) = 17,88%
2. mit Korrektur: P(X ≥ 480) = Φ((470-0,5-480)/√23,75) ≈ Φ(-0,92) = 1 - Φ(0,92) = 17,88%
3. ohne Korrektur: P(470 ≤ X ≤ 485) ≈ Φ(2,05) - Φ(-1,03) = 82,83%
   mit Korrektur: P(470 ≤ X ≤ 485) ≈ Φ(2,15) - Φ(-1,13) = 85,50%

Bild links: Diese Darstellung zeigt Teilaufgabe c mit P(470 ≤ X ≤ 485).
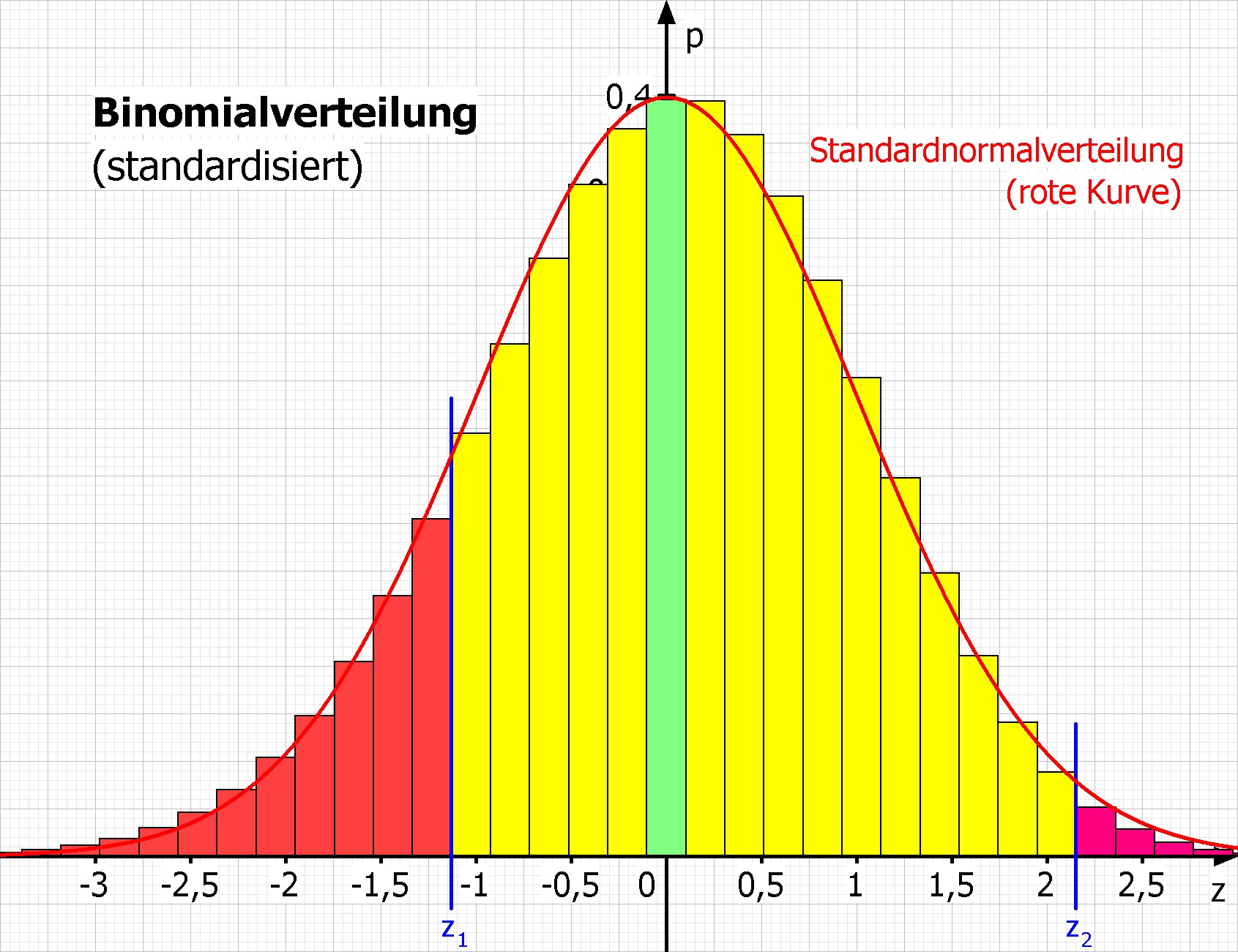
Bild rechts: Das Histogramm von Teilaufgabe c zeigt die standardisierte Binomialverteilung, darüber wurde (rote Kurve) die Normalverteilung gelegt. Die transformierten Grenzen werden als Senkrechte (blau) dargestellt.

Download MatheGrafix-Dateien

Lösung  I.c: Binomialverteilung mit Tabellen
Lösung II.c: Binomialverteilung über Näherungsformel mit Korrektur
Lösung II.c: Standardisierte Binomialverteilung

Download Webseite als Word-Text

Verteilungen: Aufgaben und Lösungen