MatheGrafix 12 / Online-Hilfe

I. Aufgabe: Ziehen mit oder ohne Zurücklegen aus einer Urne

Eine Urne enthält 3 rote und 5 grüne Kugeln. Zwei Kugeln werden nacheinander mit (ohne) Zurücklegen gezogen.

1. Berechnen Sie die Wahrscheinlichkeit, zweimal eine rote Kugel zu ziehen.
2. Berechnen Sie die Wahrscheinlichkeit, dass die zweite Kugel rot ist.

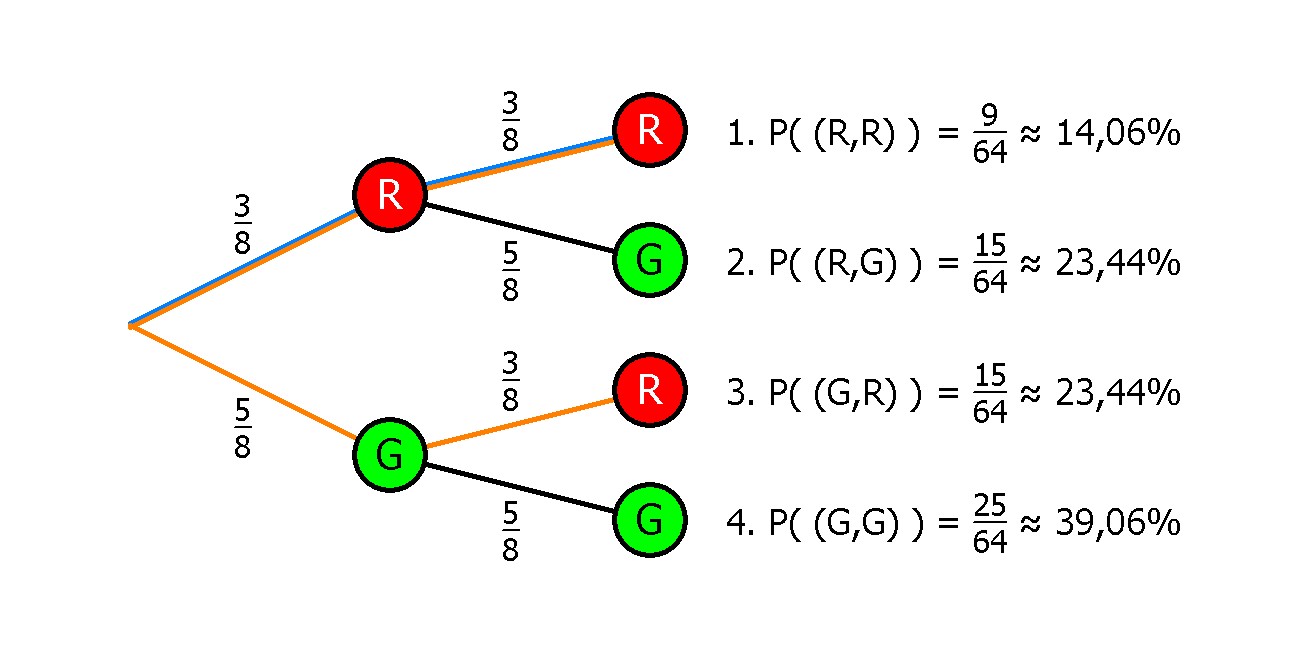Lösung: Ziehen mit Zurücklegen

1. Die Wahrscheinlichkeit, dass zwei rote Kugeln gezogen werden, beträgt nach den Pfadregeln (blauer Pfad):
   3/8 * 3/8 ≈ 14,06%.
2. Die Wahrscheinlichkeit, dass die zweite gezogene Kugel rot ist, beträgt nach den Pfadregeln (orange Pfade):
   3/8 * 3/8 + 5/8 * 3/8 = 37,5%.

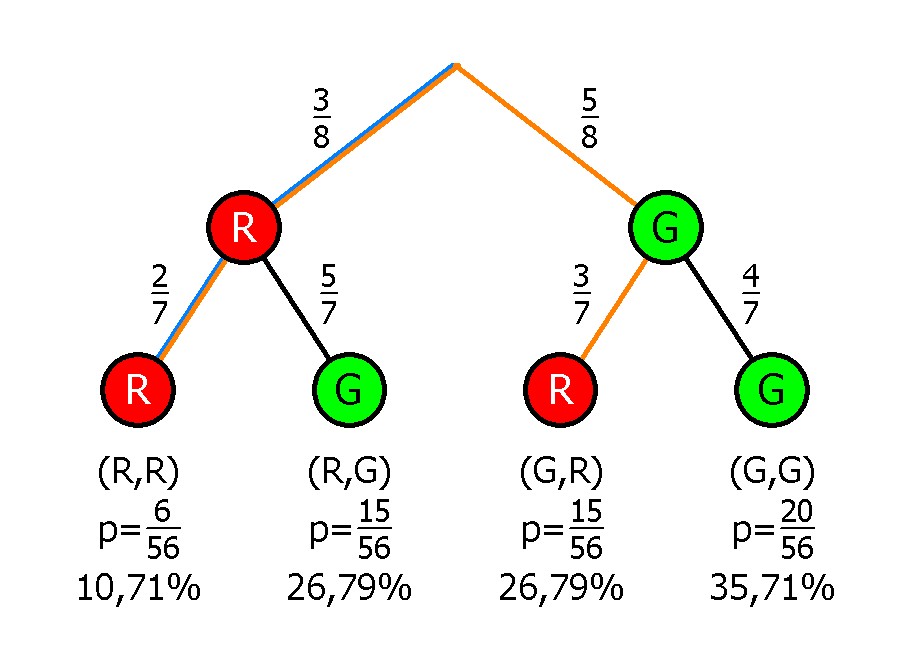Lösung: Ziehen ohne Zurücklegen

1. Die Wahrscheinlichkeit, dass zwei rote Kugeln gezogen werden, beträgt nach den Pfadregeln (blauer Pfad):
   3/8 * 2/7 ≈ 10,71%.
2. Die Wahrscheinlichkeit, dass die zweite gezogene Kugel rot ist, beträgt nach den Pfadregeln (orange Pfade):
   3/8 * 2/7 + 5/8 * 3/7 = 37,5%.

Download MatheGrafix-Dateien
Lösung: Ziehen mit Zurücklegen
Lösung: Ziehen ohne Zurücklegen

II. Aufgabe: Ein Würfel wird dreimal geworfen (Lösung mit Urnenmodell)

Ein Würfel wird dreimal nacheinander geworfen. Mit welcher Wahrscheinlichkeit würfelt man dabei

1. keine Sechs?
2. mindestens eine Sechs?
3. genau eine Sechs?
4. in den ersten beiden Würfen eine Sechs??

Diese Aufgabe ist ein Beispiel zu einem vereinfachtem Baumdiagramm (Ereignis – Gegenereignis): Bei jedem Wurf sind hierbei nur das Ereignis „Es fällt eine 6“ und das Gegenereignis „Es fällt keine 6“ dargestellt.

Lösung mit Hilfe eines Baumdiagramms

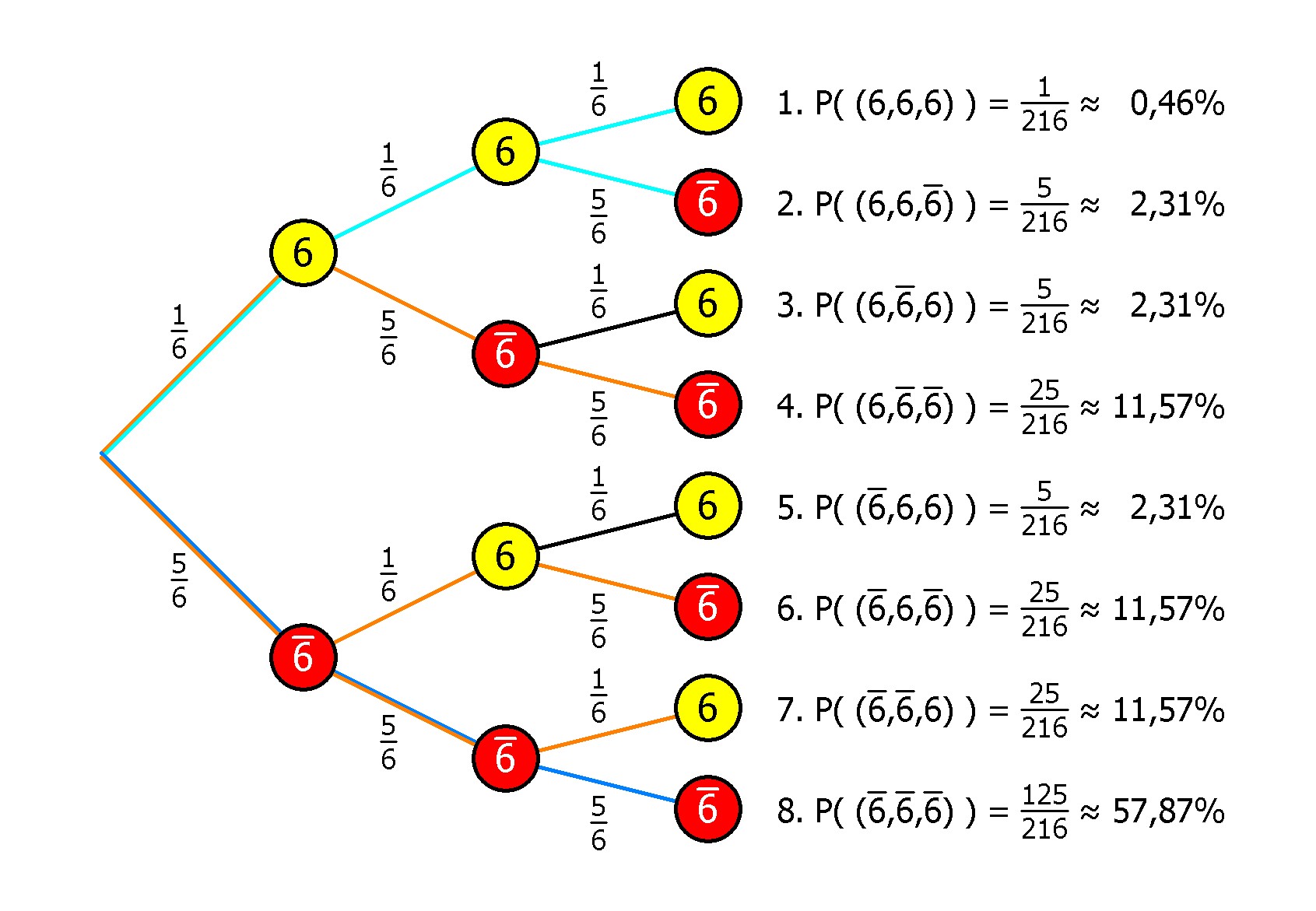
1. „Keine Sechs“ wird mit einer Wahrscheinlichkeit von
   125/216 ≈ 57,87% gewürfelt (blauer Pfad).
2. „Mindestens eine Sechs“ ist das Gegenereignis von „Keine Sechs“ und wird mit einer Wahrscheinlichkeit von
   1 - 125/216 ≈ 42,13% gewürfelt (1-Ergebnis von Teilaufgabe a).
3. „Genau eine Sechs“ wird mit einer Wahrscheinlichkeit von 25/216 + 25/216 + 25/216 ≈ 34,72% gewürfelt (orange Pfade).
4. „in den ersten beiden Würfen eine Sechs“ wird mit einer Wahrscheinlichkeit von
   1/216 + 5/216 = 1/36 ≈ 2,78% gewürfelt (hellblaue Pfade).
   Diese Teilaufgabe d lässt sich vereinfacht darstellen wie in der ersten Aufgaben auf der Seite Aufgaben: Bäume selbst zeichnen, da der dritte Wurf in dieser Teilaufgabe keine Bedeutung hat.

Download MatheGrafix-Datei: Ein Würfel wird dreimal geworfen

III. Aufgabe: Single-Choice-Test (Lösung mit Urnenmodell)

Unter Single-Choice-Aufgaben(Einfach-Wahl-Aufgaben) werden Aufgaben verstanden, bei der der Prüfling aus den vorgegebenen Antwortoptionen exakt eine richtige Antwort auswählen soll. Bei einem Test kann man nun bei drei Fragen zwischen vier vorgegebenen Antworten wählen, von denen jeweils genau eine Antwort richtig (r) ist, die anderen drei sind falsch (f). Wenn man nicht weiß, welche Antwort richtig ist, kann man auch raten. Wie groß ist die Wahrscheinlichkeit, dass man bei dem Test nur durch Raten

1. genau zwei Antworten richtig hat?
2. nur eine Antwort richtig hat?
3. mindestens eine Antwort richtig hat?

Lösung: vereinfachtes Baumdiagramm mit Hilfe des Gegenereignisses

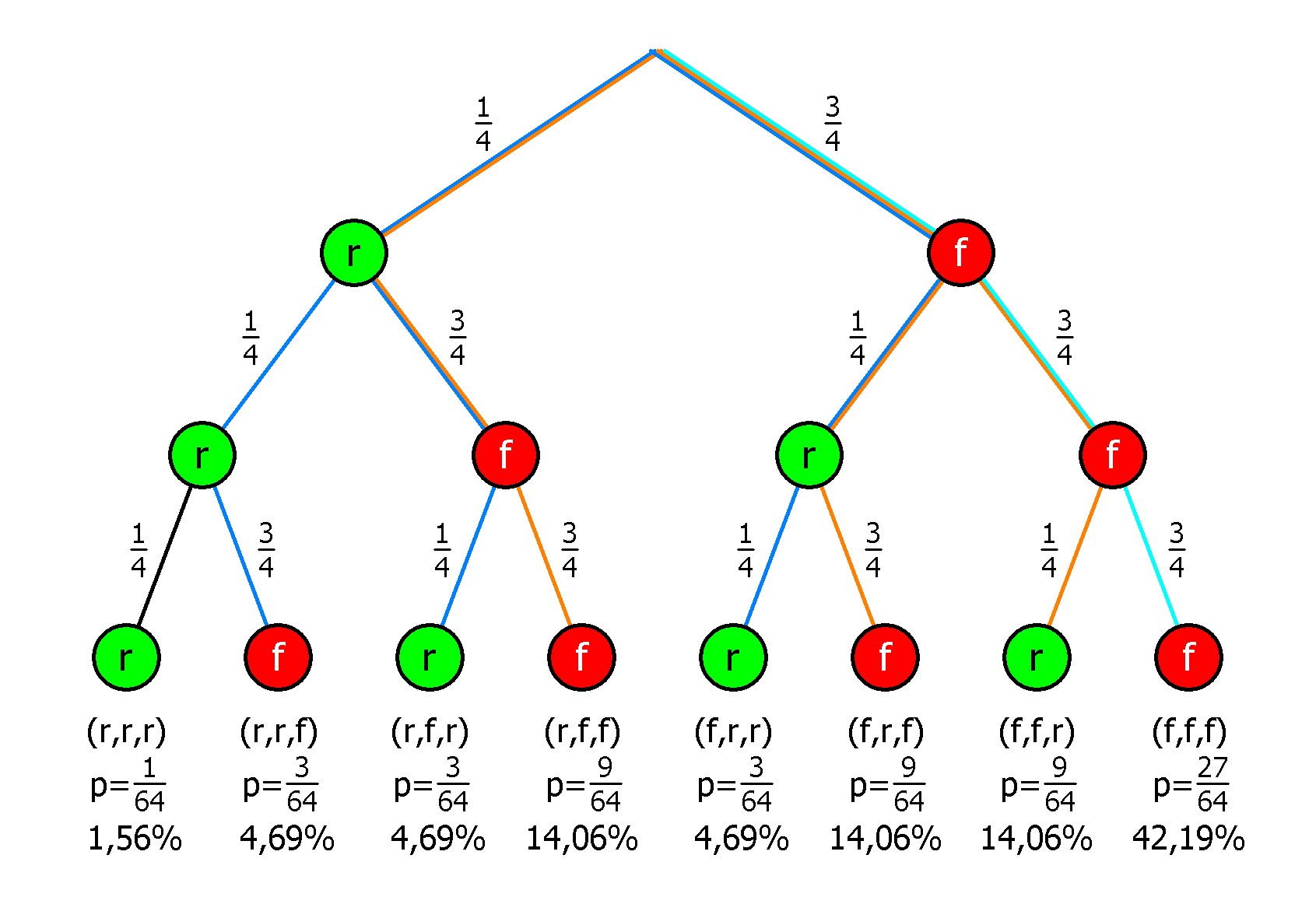
1. Genau zwei Antworten sind richtig, wenn die Ergebnisse (r,r,f), (r,f,r) und (f,r,r) eintreten. Hierfür beträgt die Wahrscheinlichkeit nach den Pfadregeln (blaue Pfade)
   3/64 + 3/64 + 3/64 ≈ 14,06%.
2. Genau eine Antwort ist richtig, wenn die Ergebnisse (r,f,f), (f,r,f) und (f,f,r) eintreten. Hierfür beträgt die Wahrscheinlichkeit nach den Pfadregeln (orange Pfade)
   9/64 + 9/64 + 9/64 ≈ 42,19%.
3. Mindestens eine Antwort ist richtig, wenn das Gegenereignis zum Ergebnis (f,f,f) eintritt. Für das Ergebnis (f,f,f) ergibt sich nach der Pfadregel die Wahrscheinlichkeit 27/64. Die Wahrscheinlichkeit für das Gegenereignis ist dann (hellblauer Pfad) 1 – 27/64 ≈ 57,81%.

Download MatheGrafix-Datei: Single-Choice-Aufgabe

Download Webseite als Word-Text: Bäume: Aufgaben und Lösungen