MatheGrafix 12 / Online-Hilfe

I. Aufgabe: Teilbaum (Baum selbst zeichnen oder Lösung mit Urnenmodell)

Es werden zwei Würfel geworfen. Mit welcher Wahrscheinlichkeit fällt ein Sechserpasch?

Lösung mit selbst gezeichnetem Teilbaum oder mit vollständigem Baum aus dem Urnenmodell:

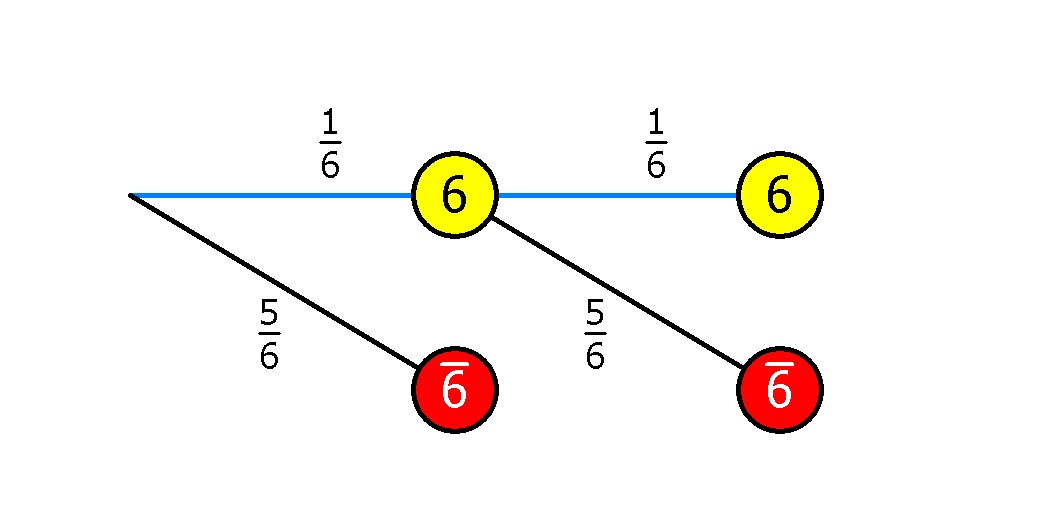
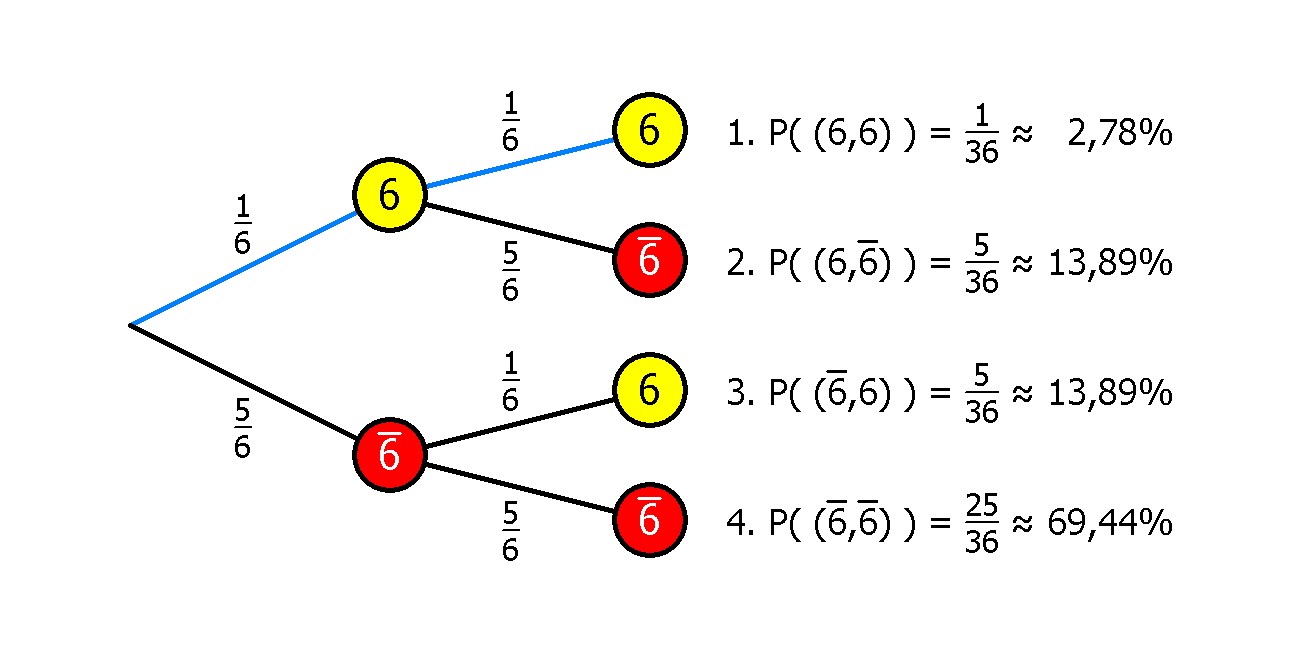Die Wahrscheinlichkeit für einen Sechserpasch beträgt nach den Pfadregeln (blauer Pfad):
1/6 * 1/6 ≈ 2,78%.

Bei jedem Wurf sind hierbei nur das Ereignis „Es fällt eine 6“ und das Gegenereignis „Es fällt keine 6“ dargestellt. Der gewünschte Pfad lässt sich bei beiden Darstellungen markieren.

• Der selbst gezeichnete Teilbaum blendet die nicht benötigten Knoten aus.
• Der vollständige Baum aus dem Urnenmodell hat den Vorteil, dass die Wahrscheinlichkeiten für die Pfade automatisch berechnet werden.

Download MatheGrafix-Dateien
Lösung: selbst gezeichneter Baum
Lösung mit Urnenmodell

II. Aufgabe: Zwei verschieden Stufen im Zufallsversuch (Baum selbst zeichnen)

Ein Händler hat in einem Koffer 200 Handys einer bestimmten Marke. Davon sind 70% Originalhandys und 30% Fälschungen, die sich auf den ersten Blick nicht unterscheiden. Von den Originalhandys sind 5% defekt, von den Fälschungen sind 30% defekt.

1. Wie groß ist die Wahrscheinlichkeit, eine funktionierende Fälschung zu erhalten, wenn man ein Handy aus dem Koffer nimmt?
2. Wie groß ist die Wahrscheinlichkeit, ein defektes Handy aus dem Koffer zu nehmen?

Lösung mit selbst gezeichnetem Baum (waagerecht oder senkrecht, Prozent oder Bruch):

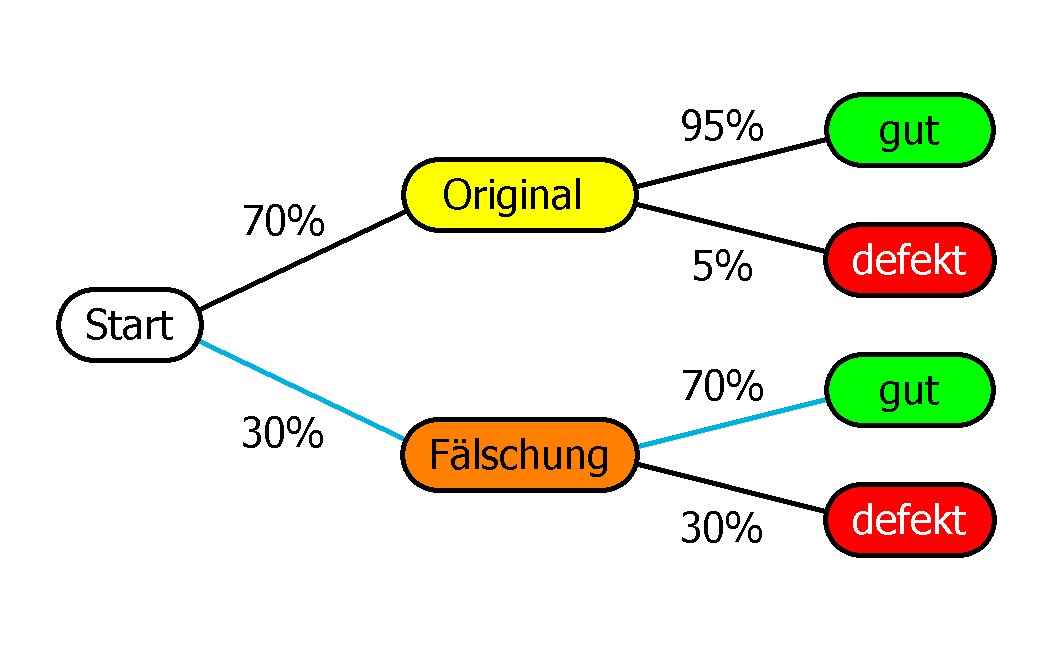
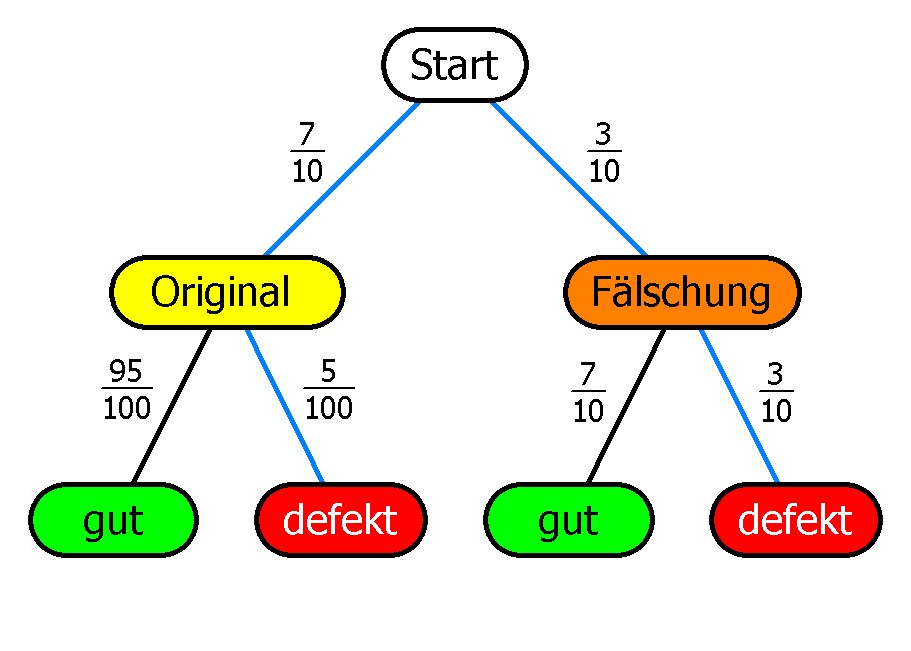
1. Die Wahrscheinlichkeit, eine funktionierende Fälschung aus dem Koffer zu nehmen, beträgt nach den Pfadregeln (blauer Pfad Bild links):
   30% * 70% = 21%.
2. Die Wahrscheinlichkeit, ein defektes Handy aus dem Koffer zu nehmen, beträgt (blaue Pfade Bild rechts):
   70% * 5% + 30% * 30% = 12,5%.

Download MatheGrafix-Dateien
Lösung mit waagerechtem Baum
Lösung mit senkrechtem Baum

Download Webseite als Word-Text

Bäume: Aufgaben und Lösungen