Startseite 
Online-Hilfe 
Impressum, Datenschutz Was ist neu in MatheGrafix 11?
Ganz neu in MatheGrafix sind das Modul Stochastik mit Wahrscheinlichkeitsbäumen und Verteilungen sowie das Raummodul mit Raumkurven, Rotationskörpern und seltsamen Attraktoren.
Viele Anregungen wurden umgesetzt bei den Einstellungen zum Koordinatensystem, den Eingabefeldern, bei der Touchbedienung, beim Exportformat (*.png) und auch bei der Darstellung auf hochauflösenden Monitoren.
Die ausführlichen Hilfeseiten zu den neuen Modulen der Version 11 werden rechts in der Navigationsleiste aufgelistet.
Stochastik
Das neue Stochastikmodul teilt sich in fünf Abteilungen:
- Erstellen von Bäumen mit dem Baumdesigner oder durch Vorgabe aus dem Urnenmodell,
- Zeichnen und Berechnen von Binomial- oder Normalverteilung und Testen von Hypothesen.
Im Stochastikmodul wurde besonderer Wert auf ausführliche Beispielaufgaben gelegt. Mit dem Youtube-Button im Programm gelangt man zu diesen Aufgaben in der Online-Hilfe.
Das Ablesen von Wahrscheinlichkeiten zur Binomial- und Normalverteilung aus den Tabellen einer Formelsammlung wird von MatheGrafix vollständig übernommen.
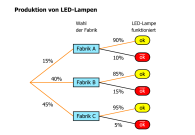Mit dem Baumdesigner, der aus Knoten- und Pfaddesigner besteht, werden Knoten und Pfade von waagerechten oder senkrechten Bäumen gestaltet. Diese Bäume können nicht "rechnen".- Bäume nach dem Urnenmodell: Aus einer Urne werden Kugeln mit oder ohne Zurücklegen gezogen. Der entsprechende Baum wird automatisch gezeichnet, dieser kann mit den von MatheGrafix berechneten Wahrscheinlichkeiten ergänzt werden.
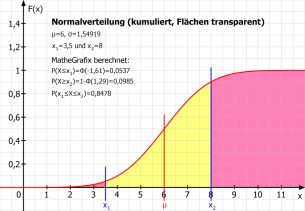Normalverteilung: Die Verteilungsfunktion und die Dichtefunktion von beliebigen Normalverteilungen oder der Standardnormalverteilung werden berechnet und dargestellt. In dieser Darstellung lassen sich Bereiche als Flächen und ausgesuchte Werte als Senkrechte markieren.
Eine Tabelle für die Standardnormalverteilung wird nicht mehr benötigt: Die Werte beliebiger Normalverteilungsfunktionen werden in MatheGrafix berechnet.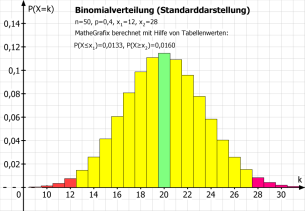
Binomialverteilungen: Beliebige Binomialverteilungen, auch kumuliert oder standardisiert, werden berechnet und gezeichnet.
Tabellen für Binomialverteilungen werden überflüssig: Die Werte der einfachen oder kumulierten Binomialverteilung werden in MatheGrafix berechnet. Diese Werte werden wahlweise "exakt" als Tabellenwert oder mit der Näherungsformel von de Moivre-Laplace berechnet.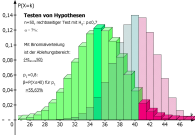
Testen von Hypothesen: Nach der Vorgabe des Testes (linksseitig, rechtsseitig oder beidseitig), der Anzahl der Versuche n, der Trefferwahrscheinlichkeit p0 und dem Signifikanzniveau α berechnet und zeichnet MatheGrafix den Ablehnungsbereich nach zwei verschiedenen Lösungsverfahren:
entweder nach den Tabellen der Binomialverteilung oder mit der Näherungsformel von de Moivre-Laplace über die Normalverteilung.
Die Darstellung der Binomialverteilung folgt dem jeweiligen Verfahren: Säulendiagramm beim Verfahren mit den Tabellen der Binomialverteilung, Stabdiagramm beim Näherungsverfahren.
Nach der Vorgabe der alternativen Wahrscheinlichkeit p1 berechnet MatheGrafix den β-Fehler und stellt die alternative Verteilung dar.
Raummodul
Das Raummodul teilt sich in vier Abteilungen:
- Zeichnen von Raumkurven und Oberflächen (jeweils ein oder zwei Parameter),
- seltsame Attraktoren als Punktwolke oder durch verbundene Linien (z.B. Lorenz-Attraktor).
- Raumkurven: Parameterkurven im Raum werden nicht durch einen expliziten Funktionsterm bestimmt, sondern durch drei Funktionen für die x-, y- und z-Auslenkung. Die Punkte einer Kurve werden als Funktion einer Variablen, dem Parameter t, durchlaufen: z.B. Strecke, Helix, Viviani-Kurve, Lissajous-Figuren.
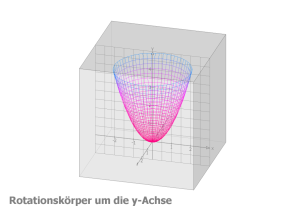Oberflächen: Flächen mit zwei Parametern werden durch drei Funktionen für die x-, y- und z-Auslenkung bestimmt. Die Punkte einer Fläche werden als Funktion zweier Variablen, den Parametern u und v, durchlaufen, z.B. Quadrat, Rotationskörper, Kleinsche Flasche, Nautilus.- Seltsame Attraktoren als Punktwolken über Zahlenfolgen: z.B. Pickover-Punktfolgen, Peter de Young-Punktfolgen.
- Seltsame Attraktoren über Differentialgleichnungen: z.B. Lorenz-Attraktor, Rössler-Attraktor.
Neues bei Einstellungen, Eingaben, Touchbedienung, hochauflösender Darstellung, Export
- Das Koordinatensystem bei Funktionen lässt sich in der Version 11 auf vielfache Weise bearbeiten: Einzelne Achsen, Zahlen oder Striche auf den Achsen werden ausgeblendet. Die Beschriftung lässt sich formatieren und ausrichten. Der Abstand der Beschriftungen kann eingestellt werden. Als Einheit der x- und y-Achse sind nun auch Pi, Pi/2, Pi/3 oder Pi/4 möglich.
- Die Eingabe von Brüchen und Vielfachen von Pi ist nun in zahlreichen Eingabefeldern möglich, z.B. beim Definitionsbereich.
- Im Bearbeitungsfenster von Punkten kann man mit einem Punktrechner die y-Koordinate eines Punktes auf einem Graphen berechnen und automatisch eintragen lassen.
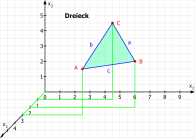Ein Heftmodus in der 3D-Geometrie hinterlegt die Grafiken mit einem einfachen 3D-Koordinatensystem und einem Karomuster. Dies entspricht der Darstellung in den Schülerheften.- Ein Touchmodus erleichtert und ermöglicht eine problemlose Bedienung auf Tablets, Smartboards oder anderen Touchscreens.
- Eine Anpassung für hochauflösende Monitore sorgt dafür, dass MatheGrafix stets in voller Schärfe dargestellt wird und nicht von Windows 10 einfach nur hochskaliert wird.
- Grafiken lassen sich zusätzlich im png-Grafikformat exportieren. Dieses Format benötigt deutlich weniger Speicherplatz als das bmp-Format, speichert aber pixelgenau (nicht wie das jpg-Format).
- Die Benutzeroberfläche wird übersichtlicher durch eine konsequente Anwendung von Tabs in allen Modulen.
